黄土高原逐年土壤侵蚀模数1-km栅格数据集
(2001–2015)
耿文广1,2,诸云强2,3,陈鹏飞2*
1. 山东理工大学建筑工程学院,淄博 255000;
2. 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室,北京 100101;
3. 江苏省地理信息资源开发与利用协同创新中心,南京
210023
摘 要:土壤侵蚀模数是衡量生态环境质量的重要指标,其时空分布数据是土壤侵蚀治理的重要科学依据。黄土高原地区是我国的生态脆弱区,水土流失严重,目前该地区还缺乏长时间序列、格式统一、完全共享的土壤侵蚀模数的数据集。为了有效支撑黄土高原地区的土壤侵蚀治理,作者基于RUSLE(The Revised Universal Soil Loss Equation)模型,通过对该地区降水、土壤质地、DEM(Digital Elevation Model)、植被指数等数据的规范化处理后,计算得到2001–2015年1-km分辨率的土壤侵蚀模数数据集。本数据集包含2001–2015年黄土高原地区逐年1-km分辨率的土壤侵蚀模数栅格数据,数据集存储格式为TIFF,由60个数据文件组成,总数据量为105.0 MB。
关键词:黄土高原;土壤侵蚀模数;RUSLE模型
DOI: https://doi.org/10.3974/geodp.2022.01.12
CSTR: https://cstr.escience.org.cn/CSTR:20146.14.2022.01.12
数据可用性声明:
本文关联实体数据集已在《全球变化数据仓储电子杂志(中英文)》出版,可获取:
https://doi.org/10.3974/geodb.2021.11.06.V1或https://cstr.escience.org.cn/CSTR:20146.11.2021.11.06.V1.
1 前言
土壤侵蚀对人类生活造成了严重影响,是我国面临的严峻环境问题,也是一个世界性问题[1–3]。黄土高原地区地形复杂、坡陡沟深、植被覆盖度低,土壤疏松、极易渗水,同时夏季多暴雨,再加上人类不合理的开发利用,导致黄土高原地区土壤侵蚀极为严重[4,5]。目前,黄土高原地区土壤侵蚀研究主要集中在单一年份、小流域或市县级尺度,缺乏长时间序列、完整空间范围、系统化的研究,严重影响黄土高原地区土壤侵蚀防治和水土保持等工作的开展。
土壤侵蚀模数数据能够帮助人们掌握区域土壤侵蚀规律,为水土流失治理工作提供重要基础。为了准确计算土壤侵蚀模数,国内外学者提出了不同的模拟计算方法。在这些计算方法中,美国农业部1997年提出的RUSLE模型(Revised Universal Soil Loess
Equation)得到了最为广泛的使用[6]。我国学者将其引入并进行了本地化的研究,优化了相关因子的计算方法使其更加适合中国的国情,这让RUSLE模型在我国的土壤侵蚀防治工作中发挥了良好的作用,同时也产生了许多开放共享的土壤侵蚀数据。
目前,已公开发表并且包含完整黄土高原地区的土壤侵蚀数据包括国家青藏高原科学数据中心[1]的《泛第三极65国1 km分辨率土壤侵蚀强度数据集(2015)》[7],该数据包含2015年泛第三极65国区域土壤侵蚀模数栅格数据;国家地球系统科学数据中心[2]的《黄土高原地区土壤侵蚀图(2010年)》,该数据为2010年黄土高原地区土壤侵蚀栅格数据;全球变化科学研究数据出版系统[3]的《中国土壤侵蚀变化数据集(1985–2011)》[8,9],该数据主要包含1985、1995、2000、2011年中国分省土壤侵蚀分级面积统计数据;还有地理国情监测云平台[4]的《全国土壤侵蚀数据》,该数据为2005年全国各省份土壤侵蚀模数数据。与此同时,已有的大量研究也生产制作了一系列不同年份和地区的黄土高原土壤侵蚀相关数据[10–12]。然而,已有的数据共享平台和相关研究的数据年份较单一,缺少长时间序列,且数据制作方法、空间分辨率及数据类型不统一,无法对黄土高原地区的土壤侵蚀做出较为系统的评价。为此,本文基于RUSLE模型生产了黄土高原区域的2001–2015年的逐年1-km土壤侵蚀模数数据集。该数据可用于分析黄土高原地区及其典型流域和土壤侵蚀类型区的水土流失时空变化特征分析,揭示黄土高原生态建设的成效,支撑土壤侵蚀时空动态变化评价、生态环境质量评价等。
2 数据集元数据简介
《黄土高原逐年土壤侵蚀模数1-km栅格数据集(2001–2015)》[13]的名称、作者、地理区域、数据年代、时间分辨率、空间分辨率、数据集组成、数据出版与共享服务平台、数据共享政策等信息见表1。
3 数据研发方法
3.1 算法原理
RULSE模型中土壤侵蚀模数是由降水数据、土壤数据、DEM(Digital Elevation Model)数据、NDVI(Normalized Difference Vegetation Index)数据和土地覆被数据计算,如式(1)所示:
A=R´K´LS´C´P (1)
式中,A为单位面积土壤侵蚀模数(t·hm–1·a–1);R为降雨侵蚀力因子(MJ·mm·hm–1·h–1·a–1);K为土壤可蚀性因子(t·h·MJ–1·mm–1);LS为坡长坡度因子;C为植被覆盖与管理因子;P为水土保持措施因子。
表1 《黄土高原逐年土壤侵蚀模数1-km栅格数据集(2001–2015)》元数据简表
|
条 目 |
描 述 |
|
数据集名称 |
黄土高原逐年土壤侵蚀模数1-km栅格数据集(2001–2015) |
|
数据集短名 |
SoilErosionLoessPlateau_2001–2015 |
|
作者信息 |
耿文广, 山东理工大学,
gengwg@lreis.ac.cn 诸云强, 中国科学院地理科学与资源研究所,
zhuyq@igsnrr.ac.cn 陈鹏飞D-7136-2019, 中国科学院地理科学与资源研究所, pengfeichen@igsnrr.ac.cn |
|
地理区域 |
黄土高原,100°E–114°E, 33°N–41°N |
|
数据年代 |
2001–2015 |
|
时间分辨率 |
年 |
|
空间分辨率 |
1 km |
|
数据格式 |
.tif |
|
数据量 |
105.0 MB(压缩后为36.2 MB) |
|
数据集组成 |
数据集由60个文件组成。文件名由SELP+年份构成,后四位数字为年份 |
|
基金项目 |
中国科学院(XDA23100100) |
|
数据计算环境 |
ArcMap |
|
出版与共享服务平台 |
全球变化科学研究数据出版系统 http://www.geodoi.ac.cn |
|
地址 |
北京市朝阳区大屯路甲11号100101,中国科学院地理科学与资源研究所 |
|
数据共享政策 |
全球变化科学研究数据出版系统的“数据”包括元数据(中英文)、通过《全球变化数据仓储电子杂志(中英文)》发表的实体数据集和通过《全球变化数据学报(中英文)》发表的数据论文。其共享政策如下:(1)“数据”以最便利的方式通过互联网系统免费向全社会开放,用户免费浏览、免费下载;(2)最终用户使用“数据”需要按照引用格式在参考文献或适当的位置标注数据来源;(3)增值服务用户或以任何形式散发和传播(包括通过计算机服务器)“数据”的用户需要与《全球变化数据学报(中英文)》编辑部签署书面协议,获得许可;(4)摘取“数据”中的部分记录创作新数据的作者需要遵循10%引用原则,即从本数据集中摘取的数据记录少于新数据集总记录量的10%,同时需要对摘取的数据记录标注数据来源[14] |
|
数据和论文检索系统 |
DOI, CSTR, Crossref, DCI, CSCD, CNKI, SciEngine, WDS/ISC, GEOSS |
降雨侵蚀力因子能够表征降雨对土壤侵蚀的影响,本研究采用了Wischmeier提出的利用月降水量计算降雨侵蚀力的经验公式[15]。土壤可蚀性因子是反映土壤对降水和地表径流敏感程度的综合指标,反映土壤被侵蚀的难易程度[16]。本文在计算土壤可蚀性因子时采用了EPIC模型方法[17],该模型考虑了土壤属性,是目前较为常用的方法。经过该模型计算得到的K值为美制单位,需要乘以常数0.131,7换算成国际通用公制单位[18]。坡长坡度因子是反映地形对土壤侵蚀影响的重要指标,本研究的坡长坡度因子采用了McCool和刘宝元等学者的研究成果[19–21]。植被覆盖管理因子表示植被覆盖和管理措施对土壤侵蚀的影响,本研究基于蔡崇法等[22]学者的方法,在计算植被覆盖度时采用了像元二分模型。水土保持措施因子是特定保持措施下的土壤流失量与相应未采取保持措施的顺坡耕作地块的土壤流失量之比值[23]。本文根据黄土高原地区已有文献研究[24–26]对水土保持措施因子其进行赋值,将林地赋值为0.8,将裸地、水体、建筑用地、草地等赋值为1;由于耕地的水土保持措施作用与坡度成正比,按照坡度范围对P进行赋值(表2)。
表2 不同坡度的耕地P值
|
坡度范围 |
P值 |
|
<5° |
0.1 |
|
5°–10° |
0.221 |
|
10°–15° |
0.305 |
|
15°–20° |
0.575 |
|
20°–25° |
0.705 |
|
>25° |
0.8 |
3.2 技术路线
黄土高原土壤侵蚀模数数据生产技术路线如图1所示,主要包括:数据收集、数据预处理、各因子计算和土壤侵蚀量计算。
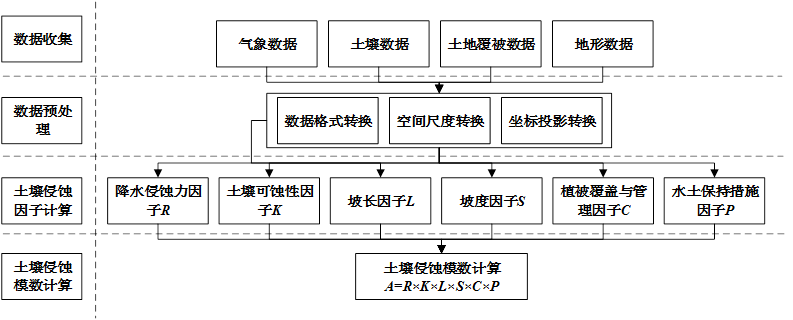
图1 数据研发技术路线图
3.2.1 数据收集与预处理
(1)降水数据来源于国家青藏高原科学数据中心的“中国区域高时空分辨率地面气象要素驱动数据集”[27,28],空间分辨率为1 km,时间分辨率为3小时。本研究选取了2001–2015年时间段数据,通过计算将其转化为月平均降水数据。
(2)土壤数据来源于国家青藏高原科学数据中心的《基于世界土壤数据库(HWSD)的中国土壤数据集(v1.1)(2009)》[29],该数据空间投影为WGS84坐标系,空间分辨率为1 km。
(3)DEM数据采用国际航天飞机雷达地形测绘任务[5](Shelter Radar Topography Mission,
SRTM)数据,空间分辨率为30 m。
(4)NDVI数据来源于美国国家航空航天局[6](NASA)基于MODIS数据反演的1-km分辨率产品(MOD13A3)。
(5)土地覆被数据采用NASA基于MODIS解译的土地覆被数据产品[7](MCD12Q1),使用该数据集时,采用了马里兰大学的土地覆被分类方法。
(6)黄土高原边界数据来源于全球变化科学研究数据出版系统的《黄土高原地区——世界地理数据大百科辞条》[30,31]。
3.2.2 数据预处理
上述数据在数据格式、坐标投影系统、空间分辨率等方面并不统一,为了便于计算,本研究采用数据格式转化、坐标投影转化、数据重采样、空间配准、裁剪等技术将数据统一在同一尺度下,即空间分辨率1 km,参考椭球体为Krasovsky,投影方式为Albers,数据格式为TIFF。
3.2.3 土壤侵蚀模数数据计算
利用经过预处理后的数据,基于RUSLE模型,分别计算降雨侵蚀力因子R、土壤可蚀性因子K、坡长因子L、坡度因子S、植被覆盖与管理因子C、水土保持措施因子P,并最终计算整个黄土高原地区2001–2015年逐年的土壤侵蚀模数,形成相关数据集。
4 数据结果与验证
4.1 数据集组成
数据集包括2001–2015年逐年共计15年的黄土高原土壤侵蚀模数数据,数据空间分辨率为1 km,参考椭球体为Krasovsky,投影方式为Albers,数据格式为TIFF,数据单位为t·hm–2·a–1。
4.2 数据结果
黄土高原2001–2015年年平均土壤侵蚀模数为37.05 t·hm–2·a–1,年均土壤侵蚀量最大为2013年的65.89
t·hm–2·a–1,最小为2015年的20.31
t·hm–2·a–1。年均土壤侵蚀量总体呈现减小的趋势,其中2001–2012年年均土壤侵蚀减小较为显著,2013年因降水量过多导致土壤侵蚀量变大。在土地覆被类型中,耕地、林地、草地的土壤侵蚀量均有减小的趋势,其中2001–2010年林地土壤侵蚀量减小最为明显。按照《土壤侵蚀分类分级标准》[32]对每年的土壤侵蚀量进行分级,将各年的土壤侵蚀数据进行对比,黄土高原地区土壤侵蚀空间分布格局大致相同。其中,2010年黄土高原土壤侵蚀模数空间分布如图2所示,从图中可以看出,黄土高原土壤侵蚀大部分处于微度或轻度侵蚀状态,但也有相当一部分处于中度及其以上的侵蚀程度。处于重度土壤侵蚀的区域主要分布在山西省北部和青海省东部地区,而处于中度土壤侵蚀的区域主要分布在黄土高原中部区域。
4.3 数据结果验证
目前,一般采用两种方法来验证模型的数据结果:一种是与实测数据进行对比,另一种是与已有研究结果对比[33]。由于实测数据取样量有限,代价成本高,且代表区域往往与基于模型计算的数据在空间上难以匹配。因此,本研究采用公开发表文献中的结果数据、公开的统计数据,对数据进行验证。
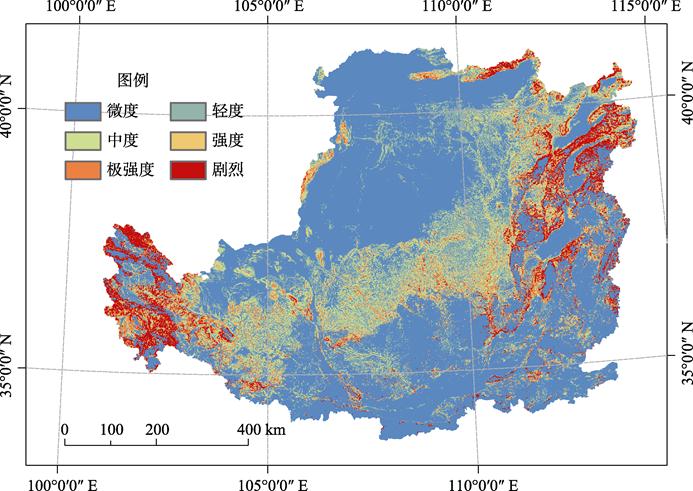
图2 2010年黄土高原土壤侵蚀空间分布图
本研究基于RUSLE模型计算的2001–2015年黄土高原地区年均土壤侵蚀模数为20.18–65.89 t·hm–2·a–1,林地的年均土壤侵蚀模数为4.87 t·hm–2·a–1,草地的年均土壤侵蚀模数为51.45 t·hm–2·a–1,耕地的年均土壤侵蚀模数为6.03 t·hm–2·a–1,城市和建筑用地的年均土壤侵蚀模数为25.36 t·hm–2·a–1。与已有研究相比(如表3所示),本研究估测的土壤侵蚀模数在正常波动范围之内。另外,从土壤侵蚀模数的空间分布规律看,本研究结果表现为黄土高原西北部和东南部主要以微度、轻度侵蚀为主,中部地区以中度侵蚀为主,山西省北部与青海省东部地区以剧烈侵蚀为主,这些规律与已有的研究结果吻合[10,12]。以上结果说明本研究制作的土壤侵蚀模数数据具有较好的准确性。
表3 已有研究结果中黄土高原土壤侵蚀数据与本研究数据的比较(t·hm–2·a–1)
|
研究区域 |
年份 |
研究方法 |
土壤侵蚀量 |
来源文献 |
本数据集的土壤侵蚀模数 |
|
长武县 |
1997–2017 |
RUSLE |
13.05–18.91 |
Yu等[34] |
5.47–37.51 |
|
榆林市 |
2000–2013 |
RUSLE |
12.18–89.69 |
杨波等[35] |
13.99–86.68 |
|
黄土高原 |
2010 |
RUSLE |
33.55 |
高海东等[10] |
35.38 |
|
黄土高原 |
年平均 |
RUSLE |
38.25 |
党星海等[11] |
37.05 |
|
黄土高原 |
2000–2010 |
RUSLE |
34.08 |
Sun等[12] |
36.40 |
注:Sun等的结果为美制单位,经过转换后得到表中数据,转换系数为2.242[36]。
5 讨论和总结
黄土高原作为我国重要的生态环境保护区,研究其土壤侵蚀规律具有重要的意义。RUSLE模型是计算土壤侵蚀模数的常用模型,具有较为明显的优势。该模型结构简单,实用性较强,预测准确度较高。此外,通过国内大量学者对RUSLE模型的不断改进,提升了模型在我国的适用性。尽管如此,RUSLE模型中的个别因子仍是经验值,有时可能会对实际情况有所偏差,易受单个因子的影响。例如本数据集中2013年土壤侵蚀量受降水数据的影响导致局部地区结果偏大。本数据集基于气象、土壤、DEM、植被指数和土地覆被数据,利用修正的土壤流失模型,整理并计算出黄土高原1-km分辨率逐年土壤侵蚀模数数据集。本数据集与以往数据集相比,其时间序列更长,空间范围更加完整。本数据集可用于掌握黄土高原土壤侵蚀的严重程度和时空分布规律,也可为黄土高原生态建设和环境管理提供数据基础。
作者分工:陈鹏飞对数据集的开发做了总体设计;耿文广收集和处理了数据,撰写了数据论文;诸云强对数据论文进行了审订修改。
利益冲突声明:本研究不存在研究者以及与公开研究成果有关的利益冲突。
参考文献
[1] 王涛. 基于RUSLE模型的土壤侵蚀影响因素定量评估:以陕北洛河流域为例[J]. 环境科学与技术, 2018, 41(8): 170–177.
[2] 殷水清, 王文婷. 土壤侵蚀研究中降雨过程随机模拟综述[J]. 地理科学进展, 2020, 39(10): 1747–1757.
[3] 姚文艺, 李勉. 黄土高原土壤侵蚀及综合治理研究评述[J]. 中国水土保持,
2005(4): 15–17.
[4] 刘国彬, 王兵, 卫伟等.
黄土高原水土流失综合治理技术及示范[J]. 生态学报, 2016, 36(22): 7074–7077.
[5] 朱显谟. 维护土壤水库确保黄土高原山川秀美[J]. 中国水土保持, 2006(1): 6–7.
[6] 陈朝良, 赵广举, 穆兴民等. 基于RUSLE模型的湟水流域土壤侵蚀时空变化[J]. 水土保持学报,
2021, 35(4): 73–79.
[7] 章文波. 泛第三极65国1-km分辨率土壤侵蚀强度数据集(2015)[Z]. 国家青藏高原科学数据中心, 2019. DOI: 10.11888/Disas.tpdc.270222.
[8] 王正兴, 李芳. 中国土壤侵蚀变化数据集(1985–2011)[DB/OL]. 全球变化数据仓储, 2018. https://doi.org/10.3974/geodb.2018.04.05.V1.
[9] 王正兴, 李芳. 中国分省土壤侵蚀变化数据集(1985–2011)[J]. 全球变化数据学报, 2018, 2(1): 51–58. https://doi.org/10.3974/geodp.2018.01.09.
[10] 高海东, 李占斌, 李鹏等. 基于土壤侵蚀控制度的黄土高原水土流失治理潜力研究[J]. 地理学报, 2015, 70(9): 1503–1515.
[11] 党星海, 孙雅杰. 地理信息系统应用下的黄土高原地区土壤侵蚀量估算[J]. 科学技术与工程, 2019, 19(25): 13–17.
[12] Sun, W. Y., Shao, Q. Q., Liu, J. Y., et al.
Assessing the effects of land use and topography on soil erosion on the Loess
Plateau in China [J]. CATENA, 2014, 121: 151–163.
[13] 耿文广, 诸云强, 陈鹏飞. 黄土高原逐年土壤侵蚀模数1-km栅格数据集(2001–2015)[J/DB/OL]. 全球变化数据仓储电子杂志, 2021. https://doi.org/10.3974/geodb.2021.11.06.V1.
https://cstr.escience.org.cn/
CSTR:20146.11.2021.11.06.V1.
[14] 全球变化科学研究数据出版系统. 全球变化科学研究数据共享政策[OL]. https://doi.org/10.3974/dp. policy.2014.05
(2017年更新).
[16] 井光花, 于兴修, 李振炜. 土壤可蚀性研究进展综述[J]. 中国水土保持, 2011(10): 44–47.
[17] Williams, J. R., Jones, C. A., Kiniry J. R., et
al. The EPIC crop growth model [J]. Transactions of the ASAE, 1989,
32(2): 497–0511.
[18]
郝姗姗,
李梦华, 马永强等. 黄土丘陵区土壤侵蚀因子敏感性分析[J]. 中国水土保持科学, 2019, 17(02): 77–86.
[19]
McCool, D.
K., Brown, L. C., Foster, G. R., et al. Revised slope steepness factor
for the universal soil loss equation [J]. Transactions of the ASAE,
1987, 30(5): 1387–1396.
[20] Liu, B. Y., Nearing, M. A., Shi, P. J., et al.
Slope Length Effects on Soil Loss for Steep Slopes [J]. Soil Science Society
of America Journal, 2000, 64(5): 1759–1763.
[21] Liu, B. Y., Nearing, M. A., Risse, M. L. Slope
gradient effects on soil loss for steep slopes [J]. Transactions of the ASAE,
1994, 37(6): 1835–1840.
[22] 蔡崇法, 丁树文, 史志华等. 应用USLE模型与地理信息系统IDRISI预测小流域土壤侵蚀量的研究[J]. 水土保持学报,
2000(2): 19–24.
[23]
刘宝元,
谢云, 张科利. 土壤侵蚀预报模型[M]. 北京: 中国科学技术出版社, 2001: 163–164.
[24]
Zhang, L.
W., Fu B. J., Lü, Y. H., et al.
Balancing multiple ecosystem services in conservation priority setting [J]. Landscape
Ecology, 2015, 30(3): 535–546.
[25] 李天宏, 郑丽娜. 基于RUSLE模型的延河流域2001–2010年土壤侵蚀动态变化[J]. 自然资源学报, 2012, 27(7): 1164–1175.
[26] 郭达, 宋小宁, 董震等. 基于RUSLE与GIS的黄土高原水土流失评价研究——以宁夏中卫地区为例[J]. 泥沙研究,
2020, 45(5): 55–60.
[27] 阳坤, 何杰. 中国区域高时空分辨率地面气象要素驱动数据集(1979–2015)[Z]. 国家青藏高原科学数据中心, 2016. DOI:
10.3972/westdc.002.2014.db.
[28] Chen, Y., Yang, K., He, J., et al.
Improving land surface temperature modeling for dry land of China [J]. Journal
of Geophysical Research:
Atmospheres, 2011, 116: D20104.
[29] Fischer, G., Nachtergaele, F., Prieler, S., et
al. Global agro-ecological zones assessment for agriculture (GAEZ 2008) [Z].
IIASA, Laxenburg, Austria and FAO, Rome, Italy, 2008.
[30] 王正兴. 黄土高原地区—世界地理数据大百科辞条[J/DB/OL]. 全球变化数据仓储, 2015.
https://doi.org/10.3974/geodb.2015.01.09.V1.
[31] 王正兴. 黄土高原地区——世界地理数据大百科辞条[J]. 全球变化数据学报, 2017, 1(1): 113.
https://doi.org/10.3974/geodp.2017.01.17.
[32] 中华人民共和国水利部. 土壤侵蚀分类分级标准: SL 190—2007 [S]. 2007.
[33] 陈鹏飞. 北纬18°以北中国陆地生态系统逐月净初级生产力1公里栅格数据集(1985–2015) [J]. 全球变化数据学报, 2019, 3(1): 34–41.
https://doi.org/10.3974/geodp.2019.01.05.
[34] Yu, S. C., Wang, F., Qu, M., et al. The
effect of land use/cover change on soil erosion change by spatial regression in
Changwu county on the Loess Plateau in China [J]. Forests, 2021, 12:
1209.
[35] 杨波, 王全九. 退耕还林后榆林市土壤侵蚀和养分流失功效研究[J]. 水土保持学报, 2016, 30(4): 57–63.
[36] 周来, 李艳洁, 孙玉军. 修正的通用土壤流失方程中各因子单位的确定[J]. 水土保持通报, 2018, 38(1): 169–174.