A Global Mountain Torque Dataset Based on Reanalysis of Three Previous Compilations
Gong, H. Huang, M.*
Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
Abstract: Mountain torque is one of the most important ways by which angular momentum is transported between the solid Earth and the atmosphere. This phenomenon is important because it can influence atmospheric circulation. We applied the method of Huang (1999) to calculate mountain torque based via reanalysis of data derived from NCEP (National Centers for Environmental Prediction), ECMWF (European Centre for Medium-Range Weather Forecasts) and MERRA (The Modem Era Retrospective analysis for Research and Applications). The dataset presented here comprises two parts: (1) anomalous mountain torque seen in Eurasia, North America, and South America over the period between 1979 and 2012; and (2) the spatial distribution of average global mountain torque between 1979 and 2012. Results showed that mountain torque spatial resolution values calculated from different reanalyzed datasets were not congruent with one another because NCEP comprised a T62 Gaussian grid encompassing 192×94 points, while ECMWF covered 0.75°×0.75° and encompassed 480×241 points, while MERRA covered 2/3°×1/2° and encompassed 540×361 points. We also integrated mountain torque from three regions in this study, Eurasia (1.5°N–77°N, 169.5°W–26°E), North America (7.5°N–71.5°N, 168°W–56°W), and South America (12°N–53.5°N, 81.5°W–35°W). This dataset is archived in .xlsx, .grd, and .nc formats with the data size of 2.53 MB in seven files (compressed to one file, 1.58 MB). The analysis related to this dataset was published in Acta Meteorologica Sinica in 2017 (Vol. 75, No. 3).
Keywords: global; mountain torque; reanalysis data; NCEP; ECMWF; MERRA; Acta Meteorologica Sinica
1 Introduction
Earth’s solid surface is not flat and encompasses a large number of rolling hills and mountains. This means that when air pressures on the eastern and western sides of mountains are inconsistent, the atmosphere generates an east-west torque referred to as “mountain torque”. This phenomenon is one of the main ways by which angular momentum is transported between the atmosphere and solid Earth[1–2]. Meteorologists were able to confirm the importance of mountain torque variation on atmospheric angular momentum balance in short timescales as early as the 1980s[3]. In early work, Ponte and Rosen[4] demonstrated how the existence of continuous positive mountain torque forced extreme peaks in atmospheric angular momentum by studying El Niño events during 1982–1983. It is also well known that the presence of mountain torque can effectively improve simulation accuracy in atmospheric models[5–7]. Therefore, an understanding of this phenomenon has become one of the most commonly applied proxies for climate monitoring and model deviation diagnosis[6,8–9].
As the main contributing factor to changes in atmospheric angular momentum, mountain torque is also important for studying atmospheric movements and Earth’s rotation. This means that high-precision, long-term mountain torque datasets are necessary for research across various fields. The data presented here encompasses both the spatial distribution and long-term variation of mountain torque around the world. These data can be applied in future research to more accurately reflect the transmission of angular momentum.
2 Metadata of Dataset
The metadata of “NCEP, ECMWF and MERRA data based global mountain torque reanalysis dataset”[10] is summarized in Table 1, including the dataset full name, short name, authors, year of dataset publication, temporal resolution, spatial resolution, data format, data size, data files, data publisher, and data sharing policy.
Table 1 Metadata summary of “NCEP, ECMWF and MERRA data based global mountain torque reanalysis dataset”
|
Items
|
Description
|
|
Dataset full name
|
NCEP, ECMWF and MERRA data based global mountain torque reanalysis dataset
|
|
Dataset short name
|
MountainTorque_1979-2012
|
|
Authors
|
Gong, H. F-8138-2015, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, hh_1@sina.com
Huang, M. W-6639-2018, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, huangm@igsnrr.ac.cn
|
|
Geographical region
|
Global
|
|
Year
|
1979–2012 Temporal resolution Annual
|
|
Spatial resolution
|
192×94, 480×241, 540×361
|
|
Data format
|
.xlsx, .grd, .nc
|
Data size
|
2.53 MB
|
|
Data files
|
The spatial distribution of global mountain torque,
Mountain torque anomalies in Eurasia, North America, and South America
|
|
Foundations
|
Ministry of Science and Technology of P. R. China (2012CB957802); National Natural Science Foundation of China (61573193)
|
|
Data publisher
|
Global Change Research Data Publishing & Repository, http://www.geodoi.ac.cn
|
|
Address
|
No. 11A, Datun Road, Chaoyang District, Beijing 100101, China
|
|
Data sharing policy
|
Data from the Global Change Research Data Publishing & Repository includes metadata, datasets (data products), and publications (in this case, in the Journal of Global Change Data & Discovery). Data sharing policy includes: (1) Data are openly available and can be freely downloaded from the Internet; (2) End users are encouraged to use Data subject to citation; (3) Users, who are by definition also value-added service providers, are welcome to redistribute Data subject to written permission from the GCdataPR Editorial Office and the issuance of a Data redistribution license; and (4) If Data are used to compile new datasets, the ‘ten percent principal’ should be followed such that Data records utilized should not surpass 10% of the new dataset contents, while sources should be clearly noted in suitable places in the new dataset[11]
|
3 Methods
3.1 Algorithm Principle
We reanalyzed NCEP (National Centers for Environmental Prediction), ECMWF (European Centre for Medium-Range Weather Forecasts), and MERRA (The Modem Era Retrospective analysis for Research and Applications) data[12] in this study in order to calculate mountain torque values for the period between 1979 and 2012 using the following equation:
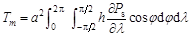 (1)
(1)
where Tm denotes global mountain torque (Hadley), a refers to the radius of the Earth (6,371 km), Ps denotes surface pressure (Pa), h is the terrain level (m), λ is longitude (o), and φ denotes latitude (o). Data from reanalysis one had a time resolution of six hours and a spatial resolution of 192×94 Gauss points. Equation (1) is therefore rewritten as follows:
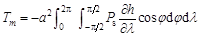 (2)
(2)
The original differential of air pressure is converted in this expression into the differential of terrain. However, as the terrain remains largely unchanged, just a single differential operation was used for all the years considered here, greatly reducing the calculation time. The Hadley unit of mountain torque is also used here (one Hadley = 1.0 × 1018 kg/m2/s2) for ease of analysis.
We used finite-difference schemes for reanalyzed grid data to calculate mountain torque[12] in all cases as follows:
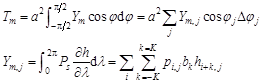 (3)
(3)
where Ym,j denotes intermediate variables for mountain torque in line j, while Δφj refers to the width (or “latitude strip”) that is dependent on grid spacing, pi,j is the surface pressure at point (i, j), hi+k,j is the geopotential at point (i+k, j), and K is 3. k values used in the finite- difference schemes were –3, –2, –1, 0, 1, 2, and 3, while the corresponding bk are –1/60, 3/20, –3/4, 0, 3/4, –3/20, and 1/60, respectively[13].
Range was selected as follows when calculating the mountain torque of particular areas: Eurasia (1.5°N–77°N, 169.5°W–26°E), North America (7.5°N–71.5°N, 168°W–56°W), and South America (12°N–53.5°N, 81.5°W–35°W). We integrated mountain torque across each selected range in order to determine annual averages for the three regions assessed here and in order to understand global changes in this variable.
3.2 Technical Route
We calculated global mountain torque for the period between 1979 and 2012 via reanalyses of NCEP, ECMWF, and MERRA data. Averaging results for intermediate years within this period enabled us to obtain average spatial distribution data for global mountain torque. We then interpolated values for three major mountain ranges to generate a time series of torque changes within each region and produced an overall dataset (Figure 1).
|
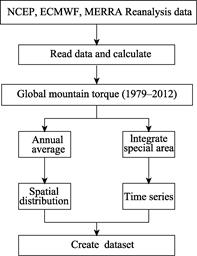
Figure 1 The process used to construct the global mountain torque dataset
|
4 Results and Validation
4.1 Data Composition
The dataset presented here includes global spatial distribution data as well as a time series for mountain torque within particular regions. These data were generated by reanalyzing NCEP, ECMWF, and MERRA values. Spatial data are archived in both .grd and .nc formats while time series data are archived in an .xlsx file.
4.2 Results
In order to facilitate future studies on mountain torque variation, we re-considered the series of values generated from our reanalysis of MERRA data. Mountain torque globally is mainly distributed in areas characterized by large terrain fluctuations (Figure 2)[14–15] such as the Andes and Rocky Mountains as well as on the Tibetan Plateau and African Plateau. Results showed that mountain torque values in South America, North America, and Central Asia varied the most. It also showed that torque was positive on the eastern side of mountain ranges or continents; thus, angular momentum is fed into the atmosphere by mountain torque. As a result, atmospheric motion is intensified, while the solid Earth loses angular momentum, and its overall rotation speed decreases. In contrast, torque values were negative on the western side of mountain ranges or continents. In this case, the atmosphere loses angular momentum through torque. As a result, atmospheric motion decelerates, and the solid Earth rotates faster. As these two phenomena can also occur simultaneously in different regions, a global integral is required prior to analysis in order to study the role of the entire atmosphere and solid Earth. Values for mountain torque are basically zero at the surface of the ocean as well as on plains and remain very small in regions with latitude higher than 60°.
There are small differences in results calculated from different reanalysis cohorts. Results calculated on the basis of NCEP data had the lowest resolution and largest spatial differences, ranging from –243 to 207 Hadley. In contrast, results calculated on the basis of MERRA data were of highest resolution and had the smallest spatial differences, ranging from –69.3 to 54.9 Hadley. Integrating mountain torque values globally also brings differences in the results from the three reanalyzed datasets; average mountain torque values for the study period calculated based on NCEP, ECMWF, and MERRA data were 1.83, –0.25, and 5.17 Hadley, respectively. However, results from the three reanalyzed datasets do reflect torque variation and exhibit basically consistent normalized curves. It is therefore beneficial to remove data error from these values in order to create a solid foundation for future research.
The data assembled here showed that the most significant spatial changes in torque occur in South America, North America, and Central Asia. We therefore integrated for these areas in order to further assess this phenomenon. Taking our results from reanalyzed MERRA data as an example (Figure 3), mountain torques within these three major regions showed an increasing trend before 2000 but then decreased after 2000, especially in South America. In the late 1980s, mountain torques fluctuated greatly, with the biggest fluctuation amplitude in Eurasia. In the study period, correlation coefficients mountain torque between global and Eurasia, North America, and South America were 0.53, 0.37, and 0.52, respectively, indicating that Qinghai-Tibet Plateau is most important for the total variance. This is consistent with previous studies[8,15].
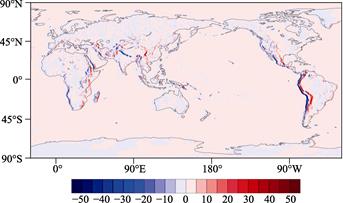
Figure 2 Spatial distribution of mountain torque by reanalysis of MERRA data during 1979–2012 (Hadley)

Figure 3 Annual average mountain torque for different areas by reanalysis of MERRA data
The level of consistency among the three sets of data varied with regions. The results were most consistent for North America, while the consistency was worst for South America. This difference might be caused by the accuracy of observation data in different regions. Generally, higher observed data accuracy leads to a better consistency of results obtained via reanalysis.
5 Conclusion
The dataset is based on reanalysis of previously collected NCEP, ECMWF, and MERRA data. We calculated values for mountain torque both globally and for particular regions in the period of 1979–2012. Global mountain torque spatial resolutions were 192×94, 480×241, and 540×361 for NCEP, ECMWF, and MERRA data, respectively. Mountain torque was mainly concentrated in areas where terrain was undulate, characterized by positive values on eastern sides and negative values on western sides. Variation in mountain torque on the Qinghai-Tibet Plateau was the most complex, and therefore most important to our understanding of global changes.
We integrated the mountain torque data in order to spatially assess a number of particular regions, namely Eurasia, South America, and North America. We also discussed changes in this variable both globally and within specific regions. The dataset provides both a high-precision spatial distribution and a time series for mountain torques. Values can be used for future Earth science studies and will prove very useful for studying both the solid Earth and atmosphere interactions.
Author Contributions
Huang, M. designed the algorithms used to generate the dataset presented here; while Gong, H. contributed to data processing, analysis, and wrote the paper.
References
[1] Weickmann, K. M., Sardeshmukh, P. D. The atmospheric angular momentum cycle associated with a Madden- Julian oscillation [J]. Journal of Atmospheric Sciences, 1994, 51(21): 3194–3208.
[2] Driscoll, S. The Earth’s atmospheric angular momentum budget and its representation in reanalysis observation datasets and climate models [D]. Berkshire: University of Reading, 2010.
[3] Swinbank, B. R. The global atmospheric angular momentum balance inferred from analyses made during the FGGE [J]. Quarterly Journal of the Royal Meteorological Society, 1985, 111(470): 977–992.
[4] Ponte, R. M., Rosen, R. D. Torques responsible for evolution of atmospheric angular momentum during the 1982-83 El Niño [J]. Journal of Atmospheric Sciences, 1999, 56(19): 3457–3462.
[5] Cess, R. D., Potter, G., Blanchet, J., et al. Intercomparison and interpretation of climate feedback processes in 19 atmospheric general circulation models [J]. Journal of Geophysical Research: Atmospheres, 1990, 95(D10): 16601–16615.
[6] Huang, H. P., Sardeshmukh, P. D., Weickmann, K. M. The balance of global angular momentum in a long-term atmospheric dataset [J]. Journal of Geophysical Research: Atmospheres, 1999, 104(D2): 2031–2040.
[7] Egger, J., Hoinka, K-P., Weickmann, K., et al. Angular momentum budgets based on NCEP and ECMWF reanalysis data: an intercomparison [J]. Monthly Weather Review, 2003, 131(11): 2577–2585.
[8] Madden, R. A., Speth, P. Estimates of atmospheric angular momentum, friction, and mountain torques during 1987–1988 [J]. Journal of the Atmospheric Sciences, 1995, 52(21): 3681–3694.
[9] Weickmann, K. M., Kiladis, G. N., Sardeshmukh, P. D. The dynamics of intraseasonal atmospheric angular momentum oscillations [J]. Journal of Atmospheric Sciences, 1997, 54(11): 1445–1461.
[10] Gong, H., Huang, M. NCEP, ECMWF and MERRA data based global mountain torque reanalysis dataset [DB/OL]. Global Change Research Data Publishing & Repository, 2018. DOI: 10.3974/geodb.2018. 06.03.V1.
[11] GCdataPR Editorial Office. GCdataPR data sharing policy [OL]. DOI: 10.3974/dp.policy.2014.05 (Updated 2017).
[12] ESRL. Physical Sciences Division, NCEP/NCAR Reanalysis 1 [OL]. https://www.esrl.noaa.gov/psd/data/
gridded/data.ncep.
[13] Huang, H. P., Weickmann, K. M. On the computation of mountain torque from gridded global datasets [J]. Monthly Weather Review, 2008, 136(10): 4005–4009.
[14] Gong, H., Zhu, L., Huang, M. Calculation and comparison of global mountain torque: a study based on three reanalysis data [J]. Acta Meteorologica Sinica, 2017, 75(3): 471–480.
[15] Wang, Y. F., Wei, D., Li, Y. Relationship between variability of the regional AAM torque and synoptic scale system over East Asia in May and June 1998 [J]. Plateau Meteorology, 2011, 30(5): 1189–1194.