Experimental Study on Optimization of Population Density Models Based on Random Forest

Liu, Y.¹  Yang, X. J.¹  Liu, J. S.^{1, 2, 3, 4*}

1. College of Resources and Environmental Sciences, Hebei Normal University, Shijiazhuang 050024, China;

2. Hebei Key Laboratory of Environmental Change and Ecological Construction, Shijiazhuang 050024, China;

3. Hebei Technology Innovation Center for Remote Sensing Identification of Environmental Change, Shijia-

zhuang 050024, China;

4. Geographic Experiment Teaching Demonstration Center of Hebei Province, Shijiazhuang 050024, China

 

Abstract: Population density is a quantitative index useful to represent the characteristics of a regional population distribution. For the last 30 years, gridded population density models have developed into an important research area in population density, and there have also been a ??Top-down demographic census data decomposition algorithm?? and a ??Bottom-up demographic survey data estimation algorithm??. Density models based on random forest (RF) modeling have been the focus of much recent attention. In this study, Shijiazhuang city is taken as an example. A preliminary comparison of multiple population density datasets revealed persistent problems, namely those of an ecological fallacy, Modifiable Areal Unit Problem (MAUP), confusion in population density patterns, and less than meticulousness in impact factor selection, among others. An optimization scheme of the models is explored in order to address the problems. In this respect, it is proposed here that random forest population density models be constructed with endowment zoning as the modeling unit, to mitigate confusion concerning the population distribution patterns. Random sampling can be applied using a hectare grid as the sampling unit, to both avoid an ecological fallacy and to overcome the effects of MAUP on the quality of samples. Mapping tests for the selection of impact factors can be constructed on a per zone basis, to avoid introducing the wrong factors into the models. This optimization scheme thus provides a more systematic approach to enhancing the reliability and validity of population density models.

Keywords: population density; random forest models; random sampling; Shijiazhuang

1 Introduction

Population density is a quantitative index widely used to represent the population distribution characteristics in a region, and a population density map is a fundamental basis for revealing population distribution patterns. Changes in population density may have important effects on regional politics, culture, resources, and environment, as well as other aspects^[1], and may be also a key driving factor in global land cover changes^[2–3]. Therefore, population density research is important fundamental work not only for the discerning of population density patterns, but also for the assessing of global change effects and disaster risk levels and formulating land space planning strategies, optimizing resource allocation^[4].

Before the 1990s, vector-format population density maps had been used in all countries of the world to represent their populations?? distribution characteristics. It was difficult to compile the vector format global population density maps with synchronized population data because of the low population census data-acquisition frequency (i.e., in many countries, one census is conducted every 10 years), low time efficiency, and inconsistent pace (disruptions from wars, plagues or other factors, left some countries unable to release census data as scheduled, or the delaying of the release)^[5–6].

The vector population density maps generally were adopted the administrative division or latitude-longitude grid as the population statistical unit^[7–8]. But neither of them matches the natural geographical unit (watershed, transect, and others) in terms of shape, size, location, and other relevant scales. In general, the conversion operation to derive population density is disturbed by the Modifiable Areal Unit Problem (MAUP)^[9–10]. It is assumed in vector-format population density maps that there is a uniform population density within the mapping units, which inadvertently conceals the true heterogeneity of all population distribution within them. For these two reasons, the real population distribution pattern is often distorted by the vector-format population density maps^[11], leading to a major undermining of the overlay analysis of population distribution along with natural, resource, environmental and other associated issues^[5]. Because raster-based analytical models are needed in global change research, the Working Group 3 of The Human Dimensions of Global Environmental Change Programme (HDP) advocated for the development of a global-gridded population density map in the early 1990s^[12].

2 Population Density Datasets

Typical population density datasets covering the whole world mainly include those of GPW (Gridded Population of the World), GRUM (Global Rural Urban Mapping Project), LandScan (LandScan Global Population Database), GHS-POP (Global Human Settlement Layer -Population), WPE (World Population Estimate), WorldPop, and HYDE (History Database of the Global Environment Population Grid). In China it is mainly the dataset of CnPOP (Table 1).

The Center for International Earth Science Information Network (CIESIN), affiliated with Columbia University, is a research institution that compiles global-gridded population density datasets^[13]. It not only independently produced the GPW population density datasets, but also jointly compiled the GRUMP, GHS-POP and WPE population density sets in cooperation with other scientific research institutions. CIESIN has produced population datasets with an areal-weighted model, now in its fourth version, which provides global population density datasets for the years 2000, 2005, 2010, 2015, and 2020, at a spatial resolution of 30 arcsec (ca. 1 km) CIESIN, in collaboration with the International Food Policy Research Institute (IFPRI), the World Bank, and the International Center for Tropical Agriculture (CIAT), has produced the GRUPM population density datasets via linear regression modeling, but there is only a first version of this. It provides global population density datasets for years 1990, 1995, and 2000, at a spatial resolution of 30 arcsec (ca. 1 km)^[14].

The European Commission Joint Research Centre (JRC), in collaboration with CIESIN, produced GHS-POP population density datasets based on a linear regression model, providing global population density datasets for years 1975, 1990, 2000, and 2015 at four different spatial resolutions^[15] (250 m, 1 km, 9 arcsec, and 30 arcsec, respectively).

The Environmental Systems Research Institute (ESRI), in collaboration with CIESIN, produced WPE population density datasets from a linear regression model, providing global population density datasets for years 2013, 2015, and 2016. Those of 2013 and 2015 are at a spatial resolution of 250 m, and that of 2016 datasets is at 150 m^[16].

The Netherlands Environmental Assessment Agency (PBL) produced HYDE population density datasets through linear regression modeling, which has evolved into a version 3.2. It provides global population density datasets from 10,000 years BC to 2016 AD, with one dataset provided for every 1,000 years spanning 10,000 to 1,000 years BC, followed by one dataset every 100 years from 0 AD to 1700 AD, then one set every 10 years from 1700 AD to 2000 AD, and most recently, with one dataset per year from 2000 to 2016. All these datasets are at a spatial resolution of 5 aremin (ca. 10 km)^[17]. Datasets from HYDE play a prominent role in the study of global change. The Oak Ridge National Laboratory (ORNL) produced LandScan population density datasets from a linear regression model, providing the annual global population density datasets for the years 2000 through 2019, at a spatial resolution of 30 arcsec (ca. 1 km)^[18]. The WorldPop, affiliated with the University of Southampton, produced WorldPop population density datasets generated using a random forest model, providing one dataset yearly from 2000 to 2020, at a spatial resolution of 30 arcsec (ca. 1 km)^[19]. The Institute of Geographic Science and Natural Resources Research, Chinese Academy of Sciences (IGSNRR, CAS), produced CnPop population density datasets through linear regression modeling, providing datasets from 2005 and 2010 of China??s population density, at a spatial resolution of 1 km^[20-21].

The above-mentioned seven major global population density sets (GPW, GRUMP, LandScan, GHS-POP, WPE, HYDE, WorldPop) have been widely applied in disaster risk assessment^[22–25], land-use change^[26–28], public health management^[29–31] and human influences on environmental changes^{[2, 32–35]}, playing a fundamental supportive role in studies of global change and environmental governance.

Scholars agree that the WorldPop population density datasets based on a random forest modeling are distinguished by higher validity^{[4, 36–37]}; hence, population density models using a random forest approach show significant advantages. In the past 30 years, Chinese scholars have also developed several gridded models of population density^{[8, 10, 37–51]}. But to date they have been only applied to China or a certain region in it. In fact, a dataset independently produced by Chinese research institutions that can encompass global population density data has yet to be produced.

3 Gridded Population Density Models

In the past 30 years, several gridded population density models have been developed, for which two categories have gradually formed: a ??top-down demographic data census algorithm?? or a ??bottom-up demographic survey data estimation algorithm??^[52].

3.1   Top-down Demographic Census Data Decomposition Algorithm

??Top-down demographic census data decomposition algorithm?? is an algorithm applied to countries or regions with good population censuses, with which the regional population total, based on deductive rules, is decomposed into individual grid, covered by the census (or population registration) units. Such algorithms mainly include an areal-weighted model^{[8, 43, 47, 53]}, distance decay model^{[38, 40, 42, 45, 54]}, linear regression model^{[2, 39, 41, 43, 46, 48-49, 55–60]}, or a random forest model^{[6, 37, 50–52, 61–62]}.

 

Table 1  Population density datasets availability (referring to^[4], with modifications)

 

3.1.1 Areal-weighted Model

Areal-weighted models are popular to be used. CIESIN has compiled the GPW with this model, lending it the advantage of being applicable in the scaling-down calculation of population density. For example, the block population vector datasets can be obtained by scaling down on the basis of the village population vector datasets of Shijiazhuang city. Then the minimal granularity population density datasets can be obtained by further scaling down on the basis of the block population vector datasets (Figure 3a). On the basis of the minimal granularity population density datasets, a scaling-up calculation of the population density can be applied with circular filtering algorithm; in this way, the MAUP problem in multi-scaled population density scaling can be systematically explored and the theory of the regional population distribution can be qualitatively constructed^[47]. The disadvantage to using this model, however, is that the heterogeneity of the population density within the grid is concealed when the gridded area is large.

3.1.2 Distant Decay Model

Distant decay model is suitable for depicting the population distribution characteristics for towns and their surrounding areas. But if the applicable conditions of the model are neglected, and they are extended to the calculation of the population density of all the regions (including villages), the validity of population density maps will be significantly reduced. This model implements an interpolation algorithm, which takes into account the distance factor, yet lacking the capability of quantitatively interpreting the mechanisms influencing population density.

3.1.3 Linear Regression Model

Linear regression model is used to generate the population density datasets produced in GRUMP by CIESIN^[14], GHS-POP by JRC and CIESIN^[15], LandScan by ORNL^[18], and WPE by ESRI^[16], HYDE by PBL^[17], and also in the CnPOP compiled by The Institute of Geographic Science and Natural Resources Research, Chinese Academy of Sciences^[20-21].

This group of models was taken into account the factors impacting population density. Due to differences regarding the factor type, the number of factors considered, and their introduction mode among various models, the resulting gridded population density datasets can differ significantly (Table 2). Such models, with the help of impact factors, are suited to construct population density datasets for countries or regions without empirical population census data. But the criterion validity of such models is not high (When calculating the population density via different models, one population density dataset is set as the criterion to which other sets are compared, whose correlation coefficient defines this criterion validity). Population density datasets compiled using such models generally have the problem of underestimating population density in urban areas while overestimating it in rural area^{[37, 63]}, which calls into question the assumption of a linear dependency between population density and its impact factors. In 2015, the Sustainable Development Goals (SDGs) held that the reliability (the consistency or stability of results obtained with the same model) and the validity (the accuracy of the populat­ion density obtained with the model) of this linear modeling approach needed improvement in the process of integrating data on population, resources, and the environment^[6].

3.1.4 Random Forest Model

During the last 5 years, random forest model has been adopted by integrating worldwide geographical data, with nonlinear dynamics in the gridded population density model, which generally leads to a improvement in the quality of the population density datasets. Random forest model is an integrated algorithm in machine learning that excels at making nonlinear calculation^[64]. The ??trees?? in the random forest are classification and regression trees (CART) constructed with training subsets of datasets, each of which is trained with the subsets constructed randomly via bootstrapping the total training sample dataset. Each CART tree is adopted to divide the mapping area into several ??type areas??, with the population distribution probability value of each type area being the average population density of all samples that fall into that area. Assuming that n CART trees are generated in the forest, it is equivalent to the formation of n independent space segmentation schemes in the graphical area. To each grid, n population distribution probability values are allocated, and their arithmetic mean per grid (i.e., the projected population distribution probability value for each grid) is then calculated. Apparently, this projected population distribution probability value always lies between the highest and lowest ones in the total training sample datasets. The Out-Of-Bag (OOB) data are also adopted in the model to measure the importance of the impact factor for population density: the greater the importance value of an impact factor is, the higher its importance will be. Because the model can be used to accurately depict the nonlinear relationships between population density and its impact factors, and to rank them in importance, it has the potential to select key impact factors acting on population density. It has become the mainstream algorithm in the production of gridded population density datasets. Random forest modeling is used by the University of Southampton of the UK in the compilation of the WorldPop population density datasets in the global scale^[19].

3.2 Bottom-up Demographic Survey Data Estimation Algorithm

It is assumed that population distribution patterns in a country lacking a population census are similar to that in surrounding countries with a census, the former??s impact factor datasets could be substituted into the random forest-based population density model of the neighboring countries, thus enabling the compilation of population density datasets for countries without a population census. To do so, population density model had been used random forest with a ??bottom-up demographic survey data estimation algorithm??.

This ??bottom-up demographic survey data estimation algorithm?? is a process in which a number of typical, miniature community population surveys are conducted in countries or regions for which no population census is available, and then combined with population density impact factor datasets for those sampled communities. The training data subsets are constructed with the communities as sampling units, and random forest models are then obtained through training. Assisted by the information in impact factor datasets, population density datasets are produced for countries and regions that currently lack a population census^[52].

3.3 Confusion in Selecting the Relevant Impact Factors

With the advent of geographic data, the impact factor datasets introduced into the gridded population density models have gradually increased (Table 2). In the creation of the LandScan, WorldPop, and HYDE datasets, the influences from natural conditions are taken into account, by incorporating datasets of annual mean temperature, annual precipitation, DEM (digital elevation model), topographic relief, land cover, and water bodies. In creating the LandScan, WPE and WorldPop datasets, the impacts of roads are taken into account, and the WorldPop dataset also adopts point-of-interest (POI) datasets^[65], to assess the impact of production, living, and consumption facilities. Because the impact factors introduced into population density models differ in terms of type, number of them used, and their introduction mode, the ensuing datasets produced by differing models tend to be significantly different. It follows that if these different datasets are consulted for the same project, their conclusions also tend to be inconsistent with each other^{[36, 66–69]}.

 

Table 2  The impact factors selected by the typical population density datasets

(referring to ^[4], with modifications)

Notes: ^a Conservation areas are not excluded from the calculation mask, but there is often zero population in these areas or no data; ^b Natural conditions include climate, topography, altitude, and so on.

 

Insufficient data has long limited the process of developing gridded population density models. To produce the world??s population density datasets, each research institution must abide by the principle of data availability, and evidently the impact factors introduced into the early gridded population density models were inevitably the product of a mutual compromise between task progress and data availability. But with the gradual improvement of geospatial data and the rapid development of spatial location services, both LandScan and WorldPop are no longer severely hindered by a shortage of impact factor datasets (Table 2). Then the questions are: which impact factors should be introduced into the gridded population density models? And how should they be introduced? Currently lacking are both theoretical guidance and a means for this selection, readily apparent in such questions as follows: What theory should be adopted to guide the selection of impact factors? What are the key factors impacting population density? Do various factors all have an impact on the global scale? Is it necessary to select factors by region? And if regional partitioning is needed, what would be the guidance for doing so?

4 Experimental Study on the Optimization of Population Density Models Based on Random Forest

Here, take Shijiazhuang region as a case study to carry out how to optimize population density models by using random forest.

4.1 General Information about the Research Region

Shijiazhuang region (including Xinji) has 12 counties, 5 county-level cities and 1 state-level high-tech development district. There are 208 townships and 64 sub-district offices, and 192 neighborhood committees, and 4,317 administrative villages. Its registered population is 9.43 million inhabitants, of which 2.32 million live in its urban areas (with 97,300 in the Jingxing mining district).

The rural population datasets were provided by the Shijiazhuang Municipal Public Security Bureau, with the summarizing time at 0:00 on May 1st, 2007. The registered population information included village names, total household number, total population, male population, female population, non-agricultural population, and agricultural population. Village boundary and block vector datasets came from the Hebei Provincial Department of Land and Resources (2006 edition). Place names data were provided by Shijiazhuang office of place names.

4.2 Exploratory Experimental Study on Random Forest-Based Population Density Models

The minimum granularity population density map (Figure 3a) was obtained with an area-weighted model, by scaling down (Figure 1). The R = 12 population density map (Figure 3b)—which used a filtering radius of 1.2 km—was obtained from a circular filtering model by scaling up, based on the minimum granularity population density map (Figure 1).

 

 

Figure 1  Flow chart for building the multi-scale population density map

The grounded theory of population distribution in Shijiazhuang region can be summarized as follows (Figure 3b.): (1) Rivers have a significant impact on surrounding population density. To avoid flooding disasters, both sides of natural rivers in plains are usually areas with a low population density; in contrast, for the convenience of gathering water, both sides of natural rivers in mountainous places are usually areas with a high population density. (2) Artificial rivers (distributaries, irrigation systems, and so on) have no significant effects on surrounding population density. (3) There is a high population density in the plains and low population density in the mountains. (4) There is high population density in cities and low population density in the countryside. (5) Both sides of the abandoned ancient natural rivers in Ming and Qing Dynasties are still areas that feature a low population density.

Figures 3c, 3d, and 3e were all obtained through calculations made with random forest- based population density models (Figure 2). They differ in that Figures 3c and 3d were obtained by sampling at the township level based on registered population data in 2007, while the Figure 3e was obtained by sampling at the county level based on census data in 2010^[19].

 

 

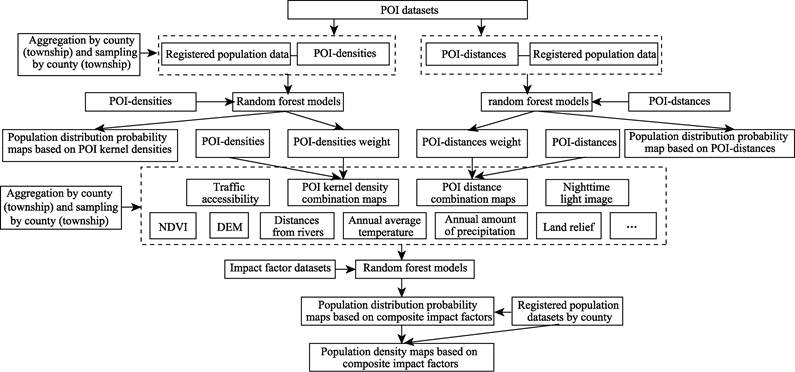
Figure 2  The calculation process of a population density model based on random forest methods

 

A phenomenon of mixed population distribution patterns was revealed by population density maps calculated using the random forest modeling approach (Figure 3d). This is the inevitable result of mixing the mountain and plain training samples in training sample datasets when the random forest-based population density models are constructed. Such problems can be overcome, at least theoretically, if mountain and plain areas are separated and respectively sampled, so that random-forest-based population density models can be constructed by zoning them accordingly.

If population density or an impact factor aggregation operation is conducted according to the administrative division units of county, township, and village, datasets of population density and impact factors in training samples must be obtained via an aggregation operation (Figure 2); hence, the quality of the training sample data will be disturbed by MAUP. For example, population density is a form of spatial constant-ratio data, whose values often vary with the statistical unit area used, a phenomenon known as the plasticity unit area of population density.

The sampling units of population density models based on random forest are mostly county, township, or other administrative division units, while the output units are mostly the kilometer grid or hectare grid. Theoretically, this phenomenon of using the analysis unit of one community to collect data while using that of another community to draw conclusions is likely to lead to the ecological fallacy problem. In population density models that are based on random forest methods (Figure 2), there is not any analysis into how or why impact factor datasets are introduced. (1) If both artificial and natural rivers are introduced indistinctly as river factors, the calculation results for sides of artificial rivers will be either low or high (Figure 3d and Figure 3e), which does not conform to the grounded theory of population distribution displayed in Figure 3b. (2) If nighttime light image is presumed to be an impact factor, a difficult problem ensues of how to overcome the blooming effect of luminous images. (3) When only 24 POI distance factors are adopted as those of impacting population density, the obtained population distribution probability map is nonetheless able to quantitatively depict the point-axis distribution characteristic of the given population (Figure 3c); this shows that the POI distance combination dataset can very well represent innovation endowment features. If they are adopted to replace nighttime light image factor, it is possible that the ??blooming effect?? of luminous images could be overcome.

 

 

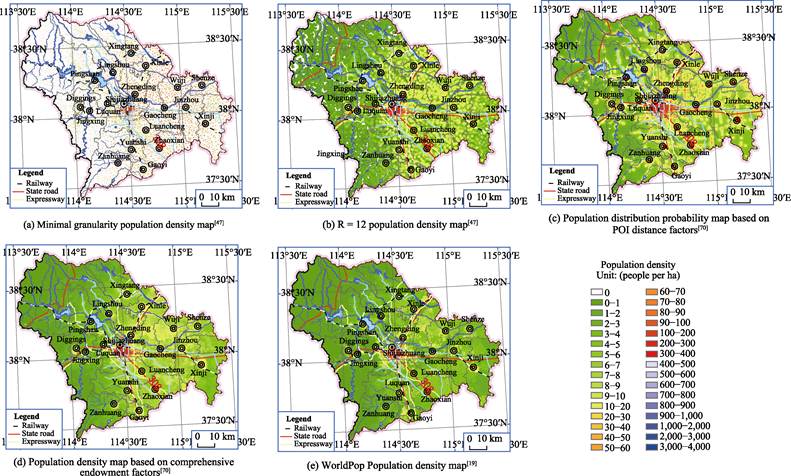
Figure 3  Map of typical population density and population distribution probability

5 Discussion and Conclusion

5.1 Discussion  

5.1.1 The Issue of Constructing Gridded Population Density Models by Zoning Method

As early as the 1980s, Mr. Hu, Huanyong clearly proposed that not only is comprehensive research needed to explore the patterning of population distributions, but proper partitioning is also essential for investigating population distribution and development patterns^[69]. Hu reckoned there is an interaction among the human population, natural resources, the economy, and science and technology. Accordingly, they must be sufficiently integrated and coordinated that it would be of little value to separately calculate any single factor With this in mind, Hu divided China into three belts and eight zones and predicted their respective population development^[71–73]. Hu??s zoning idea in the study of population geography coincides with the regional system theory of human–earth relations^[74–77] and the theory of evolutionary economic geography^[78–80], pointing to the direction and path that would deepen the study of population density. The zoning idea should be adopted in the optimization of the random forest-based population density models and in the selection of impact factors that could act on populations.

The natural geographic regionalization unit has served as the basis for knowledge exploration with data on geographical spaces. It goes beyond merely a regional division, in also being a scientific method to understand geographic features and to discover geographical patterns^[81]. Regionalization, by zoning places with the same geographical features together and categorizing places with different features into another zone, not only avoids the defects of fragmentation but also the trouble of repeated exposition^[82]. Natural geographic regionalization unit has thus become the subject and basis of exploring knowledge with geospatial data in the age of information^[81]. Population distribution is the historical accumulation of regional man–land elements?? co-evolution. The divergences in an integrated regional endowments and population development paths may lead to different population density-impacting mechanisms operating in different social development stages. Therefore, to optimize population density models based on random forest, our academic tradition of natural geographic regionalization should be innovated by the construction of advanced population density models, enabling us to compile population density maps and to explain population distribution patterns and population development patterns by region^[83].

5.1.2 How to Select Population Density Impact Factors Consistent with the Theory of Evolutionary Economic Geography

Evolutionary economic geography holds the view that in the age of agricultural civilization, natural endowments—altitude, surface roughness, water resource suitability, agricultural, agricultural potential productivity, annual mean temperature, annual precipitation, and annual evaporation—were the major factors determining regional development, whereas in the age of industrial civilization, economic endowments (i.e., traffic location and city location) were the major factors driving regional development. In the age of information civilization, it is innovation endowments (knowledge, technology, network, policy, system) which are the major factors shaping regional development^[80]. Hu Huanyong Line^[7] was the inevitable result of the land-locking effect of natural endowments upon regional development in the age of agricultural civilization, being a classic case of natural endowments?? (especially water resources) controlling population distribution patterns. In the age of industrial civilization, the comparative cost of transportation in half of northwest China was neither reduced nor was the constraint of water shortage alleviated. In the age of information civilization, innovation endowments in half of northwest China still display a point-axis distribution pattern and the comprehensive constraints of these endowments are the fundamental reason for the ??Overall stability of Hu Huangyong Line and the local adjustments of the east and west halves?? in the past 70 years^[84–90]. The population density optimization models based on random forest algorithms should inherit the classical results of comprehensive zoning^[91–92]. The theoretical results of evolutionary geography should be combined with the development stage of the region, center around natural, economic and innovation endowments adopt a combined qualitative and quantitative method and select population density impact factors. It is anticipated that Chinese population geographers will play an active role in optimizing such population density models by integrating multiple research paradigms and conducting complex geographical research^[93–94].

5.1.3 Optimization Scheme of Population Density Models Based on Random Forest

In countries or regions where comprehensive agricultural zoning has been implemented, it is encouraged that comprehensive agricultural zoning maps as well as urban and rural distribution maps be superimposed, to form comprehensive endowment zoning plans. In those countries or regions without comprehensive agricultural zoning, it is advised that geomorphic zoning maps and urban and rural distribution maps are superimposed to form alternative comprehensive endowment zoning plans. Based on the minimum granularity population density map (Figure 3a), natural (DEM, relief, distance from natural rivers, NDVI, annual mean temperature, annual amount of precipitation and so on), economic (traffic accessibility, POIs kernel density combination figures), and innovation endowment (POIs distance combination figures) datasets, one can conduct random sampling (overcoming the ecological fallacy problem, and circumventing MAUP) using the hectare grid as the analysis unit, to build training sample datasets, which are then applied in random forest modeling, enabling one to calculate population density. This is all done by zone, to avoid confusion in the population distribution quantified and its interpretation.

A series of population density mapping experiments should be carried out. Impact factors acting on population density can be screened on a per zone basis, by adding or deleting one of the factors or adjusting the sampling size, accordingly, to define the optimal sampling size of the training sample sets so as to avoid introducing erroneous factors. The optimal sampling size can be defined by zone to improve the overall reliability of the model. Combined with field investigations, qualitative and quantitative comparative analysis could be pursued to ensure the model??s validity. Finally, via the synthesis of the mapping experiment??s results, technological details of the optimization scheme for the random forest-based population density models are defined (Figure 4).

 

 

Figure 4  Optimization scheme of a population density model based on random forest method

5.2 Conclusion

In the last 30 years, with the continuous improvement of global geographical big data and the progress of machine learning algorithms, the gridded population density models have gradually evolved, shifting from interposition models, such as areal weighted and distance decay models, to linear regression and random forest models. The population density maps compiled with models based on random forest have greater accuracy, but these models are still plagued by the problems of ecological fallacy, MAUP, mixed-up population distribution patterns, and a less than-meticulousness impact factor selection.

Minimum granularity population density maps can be compiled by applying areal- weighted models based on population data of villages?? residents. The grounded theory of regional population density can be implemented by adopting filter models to carry out scaling-up calculations. Population density??s impact factors can be selected from the natural, economical, and innovation endowment factors. Random sampling by zoning can be applied, using the hectare grid as the sampling unit, to overcome the ecological fallacy problem arising from sampling unit area exceeding the output unit area and to avoid MAUP due to the aggregation operation of the training sample data. In this way, the quality of the training sample data obtained from the random forest-based population density model is greatly improved. Then a group control experiment can be conducted with that latter model to select factors impacting population density, to explore the sampling size, and to compile a population density map, all on a by-zone basis, so that the confusion in population distribution patterns on population density maps can be avoided and both the reliability and validity of the models based on random forest is further improved. The optimization scheme of such models will further promote the fundamental theoretical research on mechanisms influencing population density, patterns of population distribution, and laws of population evolution.

 

References

[1]      Wu, W. H., Niu, S. W. A comparative study on the impact of population growth and consumption increase on China??s resource-environment [J]. Chinese Journal of Population Science, 2009, 23(2): 66‒73.

[2]      Goldewijk, K. K., Ramankutty, N. Land cover change over the last three centuries due to human activities: The availability of new global data sets [J]. GeoJournal, 2004, 61(4): 335‒344.

[3]      Goldewijk, K. K., Beusen, A., Drecht, G. V., et al. The HYDE 3.1 spatially explicit database of human-induced global land-use change over the past 12,000 years [J]. Global Ecology & Biogeography, 2011, 20(1): 73‒86.

[4]      Leyk, S., Gaughan, A. E., Adamo, S. B., et al. The spatial allocation of population: a review of large-scale gridded population data products and their fitness for use [J]. Earth System Science Data, 2019, 11(3): 1385‒1409.

[5]      Bai, Z. Q., Wang, J. L., Yang, F. Research progress in spatialization of population data [J]. Progress in Geography, 2013, 32(11): 1692–1702.

[6]      Tatem, A. J. WorldPop, open data for spatial demography [J]. Scientific Data, 2017, 4(1): 1‒4.

[7]      Hu, H. Y. The distribution of population in China: with statistics and maps [J]. Acta Geographica Sinica, 1935, 2(2): 33‒74.

[8]      Zhang, C. X. Using latitude and longitude grid cells to compile a population density map: taking the Beijing-Tianjin-Tangshan area as an example [J]. Areal Research and Development, 1985, 4(2): 57‒66.

[9]      Openshaw, S. The Modifiable Areal Unit Problem [M]. Norwich, UK: Geobooks, 1983.

[10]   Yang, X. H., Jiang, D., Wang, N. B., et al. Method of pixelizing population data [J]. Acta Geographica Sinica, 2002, 57(0z1): 70‒75.

[11]   Liu, J. S., Wang, W., Xiang, H. B. The computational model of multi-scale population density [C]. International Conference on Geoinformatics, 2011: 1‒4.

[12]   Clarke, J. I., Rhind, D. W., Becket, C., et al. Population data and global environmental change [Z]. Barcelona Spain International Social Science Council Human Dimensions of Global Environmental Change Programme, 1992, 3(2): 147

[13]   Center for International Earth Science Information Network (CIESIN), Columbia University. Documentation for the gridded population of the world, version 4 (GPWv4), revision 11 data sets [EB/OL]. NASA Socioeconomic Data and Applications Center (SEDAC). https://sedac.ciesin.columbia.edu/downloads/docs/ gpw-v4/gpw-v4-documentation-rev11.pdf.

[14]   Center for International Earth Science Information Network (CIESIN, Columbia University), International Food Policy Research Institute (IFPRI), The World Bank, et al. Global rural-urban mapping project, version 1: population density grid [EB/OL]. NASA Socioeconomic Data and Applications Center (SEDAC). https://sedac.ciesin.columbia.edu/data/set/grump-v1-population-density.

[15]   Florczyk, A. J., Corbane, C., Ehrlich, D., et al. GHSL data package 2019 [EB/OL]. European Commission Joint Research Center. https://ghsl.jrc.ec.europa.eu/documents/GHSL_Data_Package_2019.pdf?t= 1478q532234372.

[16]   Frye, C., Wright, D. J., Nordstrand, E., et al. Using classified and unclassified land cover data to estimate the footprint of human settlement [J]. Data Science Journal, 2018, 17(4): 1‒12.

[17]   Goldewijk, K. K., Beusen, A., Janssen, P. Long-term dynamic modeling of global population and built-up area in a spatially explicit way: HYDE 3.1 [J]. The Holocene, 2010, 20(4): 565‒573.

[18]   Oak Ridge National Laboratory. LandScan datasets [EB/OL]. UT-Battelle for the Department of Energy. https://landscan.ornl.gov/landscan-datasets.

[19]   WorldPop, University of Southampton. Population density [EB/OL]. School of Geography and Environmental Science, University of Southampton; Department of Geography and Geosciences, University of Louisville; Departement de Geographie, Universite de Namur, Center for International Earth Science Information Network (CIESIN), Columbia University. https://www.worldpop.org/project/categories?id=18.

[20]   Fu, J. Y., Jiang, D., Huang, Y. H. 1 km grid population dataset of China (2005, 2010) [J]. Acta Geographica Sinica, 2014, 69(s1): 41‒44.

[21]   Fu, J. Y., Jiang, D., Huang, Y. H. 1 km grid population dataset of China [J/DB/OL]. Digital Journal of Global Change Data Repository, 2014. https://doi.org/10.3974/geodb.2014.01.06.V1.

[22]   Smith, K. We are seven billion [J]. Nature Climate Change, 2011, 1(7): 331‒335.

[23]   World Resources Institute (WRI). World resources 2010–2011: Decision making in a changing climate — adaptation challenges and choices [J]. Executive Summary, 2011, 4(6): 305.

[24]   Gleeson, T., Wada, Y., Bierkens, M. F. P., et al. Water balance of global aquifers revealed by groundwater footprint [J]. Nature, 2012, 488(7410): 197‒200.

[25]   Kibret, S., Lautze, J., Mccartney, M., et al. Malaria impact of large dams in sub-Saharan Africa: Maps, estimates and predictions [J]. Malaria Journal, 2015, 14(1): 339.

[26]   Goldewijk, K. K. Three centuries of global population growth: a spatial referenced population (density) database for 1700–2000 [J]. Population and Environment, 2005, 26(4): 343‒367.

[27]   Seto, K. C., Guneralp, B., Hutyra, R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools [J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(40): 16083‒16088.

[28]   Melchiorri, M., Florczyk, A. J., Freire, S., et al. Unveiling 25 years of planetary urbanization with remote sensing: Perspectives from the global human settlement layer [J]. Remote Sensing, 2018, 10(5): 768.

[29]   Sorichetta, A., Bird, T. J., Ruktanonchai, N. W., et al. Mapping internal connectivity through human migration in malaria endemic countries [J]. Scientific Data, 2016, 3(1): 5‒11.

[30]   Ouma, P. O., Maina, J., Thuranira, P. N., et al. Access to emergency hospital care provided by the public sector in sub-Saharan Africa in 2015: a geocoded inventory and spatial analysis [J]. The Lancet Glob Health, 2018, 6(3): 342‒350.

[31]   Thomson, D. R., Linard, C., Vanhuysse, S., et al. Extending data for urban health decision-making: A menu of new and potential neighborhood-level health determinants datasets in LMICs [J]. Journal of Urban Health-bulletin of the New York Academy of Medicine, 2019, 96(4): 514‒536.

[32]   Gaston, K. J., Blackburn, T. M., Goldewijk, K. K. Habitat conversion and global avian biodiversity loss [J]. Proceedings of the Royal Society B: Biological Sciences, 2003, 270(1521): 1293‒1300.

[33]   Houweling, S., VanderWerf, G. R., Goldewijk, K. K., et al. Early anthropogenic CH₄ emissions and the variation of CH₄ and ¹³CH₄ over the last millennium [J]. Global Biogeochemical Cycles, 2008, 22(1): 1‒21.

[34]   Ellis, E. C., Goldewijk, K. K., Siebert, S., et al. Anthropogenic transformation of the biomes, 1700 to 2000 [J]. Global Ecology & Biogeography Letters, 2010, 19(5): 589‒606.

[35]   Maisels, F., Strindberg, S., Blake, S., et al. Devastating decline of forest elephants in Central Africa [J]. PLoS One, 2013, 8(3): 1‒17.

[36]   Bai, Z. Q., Wang, J. L., Wang, M. M., et al. Accuracy assessment of multi-source gridded population distribution datasets in China [J]. Sustainability, 2018, 10(5): 1363‒1378.

[37]   Ye, T. T., Zhao, N. Z., Yang, X. C., et al. Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model [J]. Science of the Total Environment, 2019, 658: 936‒946.

[38]   Wang, F. H., Guldmann, J. M. Simulating urban population density with a gravity-based model [J]. Socio-economic Planning Sciences, 1996, 30(4): 245‒256.

[39]   Lo, C. P. Modeling the population of China using DMSP operational linescan system nighttime data [J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(9): 1037‒1047.

[40]   Feng, J. Modeling the spatial distribution of urban population density and its evolution in Hangzhou [J]. Geographical Research, 2002, 21(5): 635‒646.

[41]   Jiang, D., Yang, X. H., Wang, N. B., et al. Study on spatial distribution of population based on remote sensing and GIS [J]. Advances in Earth Science, 2002, 17 (5): 734‒738.

[42]   Liu, J. Y., Yue, T. X., Wang, A. Y., et al. Digital simulation of population density in China [J]. Acta Geographica Sinica, 2003(1): 17‒24.

[43]   Jin, J., Li, C. M., Yin, J., et al. Investigation on the model for spatial distribution of population data [J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 278‒282.

[44]   Tian, Y. Z., Chen, S. P., Yue, T. X., et al. Simulation of Chinese population density based on land use [J]. Acta Geographica Sinica, 2004, 59(2): 283‒292.

[45]   Yue, T. X., Wang, Y. A., Liu, J. Y., et al. Surface modeling of human population distribution in China [J]. Ecological Modelling, 2005, 181(4): 461‒478.

[46]   Zhuo, L., Chen, J., Shi, P. J., et al. Modeling population density of China in 1998 based on DMSP/OLS nighttime light image [J]. Acta Geographica Sinica, 2005, 60(2): 266‒276.

[47]   Liu, J. S. The geographical meaning about the modifiable areal unit problem in the population density

scaling [D]. Shijiazhuang: Hebei Normal University, 2009.

[48]   Zeng, C. Q., Zhou, Y., Wang, S. X., et al. Population spatialization in China based on night-time imagery and land use data [J]. International Journal of Remote Sensing, 2011, 32(24): 9599‒9620.

[49]   Gao, Y., Wang, H., Wang, P. T., et al. Population spatial processing for Chinese coastal zones based on census and multiple night light data [J]. Resources Science, 2013, 35(12): 2517‒2523.

[50]   Tan, M., Liu, K., Liu, L., et al. Spatialization of population in the Pearl River Delta in 30 m grids using random forest model [J]. Progress in Geography, 2017, 36(10): 1304‒1312.

[51]   Wang, C., Kan, A. K., Zeng, Y. L., et al. Population distribution pattern and influencing factors in Tibet based on random forest model [J]. Acta Geographica Sinica, 2019, 74(4): 664‒680.

[52]   Wardrop, N. A., Jochem, W. C., Bird, T. J., et al. Spatially disaggregated population estimates in the absence of national population and housing census data [J]. Proceedings of the National Academy of Sciences of the United States of America, 2018, 115(14): 3529‒3537.

[53]   Tobler, W., Deichmann, U., Gottsegen, J., et al. World population in a grid of spherical quadrilaterals [J]. International Journal of Population Geography, 1997, 3(3): 203‒225

[54]   Clark, C. Urban population densities [J]. Journal of the Royal Statistical Society, 1951, 114(4): 490‒496.

[55]   Sutton, P. Modeling population density with night-time satellite imagery and GIS [J]. Computers Environment & Urban Systems, 1997, 21(3/4): 227‒244.

[56]   Sutton, P., Roberts, D., Elvidge, C., et al. A comparison of nighttime satellite imagery and population density for the Continental United States [J]. Photogrammetric Engineering and Remote Sensing, 1997, 63(11): 1303‒1313.

[57]   Dobson, J. E., Bright, E. A., Coleman, P. R., et al. LandScan: a global population database for estimating populations at risk [J]. Photogrammetric Engineering and Remote Sensing, 2000, 66(7): 849‒857.

[58]   Amaral, S., Monteiro, A. M. V., Câmara, G., et al. DMSP/OLS night-time light imagery for urban population estimates in the Brazilian Amazon [J]. International Journal of Remote Sensing, 2006, 27(5): 855‒870.

[59]   Bhaduri, B., Bright. E., Coleman, P., et al. LandScan USA: a high-resolution geospatial and temporal modeling approach for population distribution and dynamics [J]. GeoJournal, 2007, 69(1/2): 103‒117.

[60]   Briggs, D. J., Gulliver, J., Fecht, D., et al. Dasymetric modelling of small-area population distribution using land cover and light emissions data [J]. Remote Sensing of Environment, 2007, 108(4): 451‒466.

[61]   Stevens, F. R., Gaughan, A. E., Linard, C., et al. Disaggregating census data for population mapping using random forests with remotely-sensed and ancillary data [J]. PLoS One, 2015, 10(2): 1‒22.

[62]   Gaughan, A. E., Stevens, F. R., Huang, Z., et al. Spatiotemporal patterns of population in mainland China, 1990 to 2010 [J]. Scientific Data, 2016, 3(1): 1‒11.

[63]   Yang, X. C., Yue, W. Z., Gao, D. W. Spatial improvement of human population distribution based on multi-sensor remote-sensing data: an input for exposure assessment [J]. International Journal of Remote Sensing, 2013, 34(15): 5569‒5583.

[64]   Breiman, L. Random forests [J]. Machine Learning, 2001, 45(1): 5‒32.

[65]   Bakillah, M., Liang, S., Mobasheri, A., et al. Fine-resolution population mapping using OpenStreetMap points-of-interest [J]. International Journal of Geographical Information Science, 2014, 28(9): 1940‒1963.

[66]   Hay, S. I., Noor, A. M., Nelson, A., et al. The accuracy of human population maps for public health application [J]. Tropical Medicine & International Health, 2005, 10(10): 1073‒1086.

[67]   Balk, D. L., Deichmann, U., Yetman, G., et al. Determining global population distribution: methods, applications and data [J]. Advances in Parasitology, 2006, 7(62): 119‒156.

[68]   Mondal, P., Tatem, A. J. Uncertainties in measuring populations potentially impacted by sea level rise and coastal flooding [J]. PLoS One, 2012, 7(10): 1‒7.

[69]   Smith, A., Bates, P. D., Wing, O., et al. New estimates of flood exposure in developing countries using high-resolution population data [J]. Nature Communications, 2019, 10(1): 1‒7.

[70]   Wang, Y. Study of population density based on random forest model [D]. Shijiazhuang: Hebei Normal University, 2020.

[71]   Hu, H. Y. The distribution, regionalization and prospect of China??s population [J]. Acta Geographica Sinica, 1990, 45(2): 139‒145.

[72]   Hu, H. Y. The Past and Future of Population Growth and Economic Development in the Eight Regions of China [M]. Shanghai: East China Normal University Press, 1986.

[73]   Hu, H. Y. Population, Economy and Ecological Environment in the Three Belts of Eastern, Central and Western China [M]. Shanghai: East China Normal University Press, 1989.

[74]   Wu, C. J. The core of study of geography: man-land relationship areal system [J]. Economic Geography, 1991, 11(3): 1–6.

[75]   Fan, J. Comprehensiveness of geography and integrated research on regional development [J]. Acta Geographica Sinica, 2004, 59(S1): 33‒40.

[76]   Fan, J. Academic thinking and economic geography of the ??regional system of man-land relationship?? [J]. Economic Geography, 2008, 28(2): 870‒878.

[77]   Fan, J. The progress and characteristics of Chinese human geography over the past 70 years [J]. Scientia Sinica Terrae, 2019, 49(11): 1697–1719.

[78]   Krugman, P. First nature, second nature, and metropolitan location [J]. Journal of Regional Science, 1993, 33(2): 129‒144.

[79]   Lu, D. D. New factors and new patterns of regional development in China [J]. Geographical Research, 2003, 22(3): 261‒271.

[80]   Xia, H. B., Wang, Z. Evolution of land differentiation in Chinese mainland [J]. Geographical Research, 2012, 31(12): 2123‒2138.

[81]   Zheng, D., Ou, Y., Zhou, C. H. Understanding of and thinking over geographical regionalization methodology [J]. Acta Geographica Sinica, 2008, 6(3): 563‒573.

[82]   Editing Group of Collections of Huang Bingwei. Integrated Studies of Geography: Collections of Huang Bingwei [M]. Beijing: The Commercial Press, 2003.

[83]   Liu, C. M., Zheng, D., Lu, D. D., et al. Development orientations for geographical sciences: written speeches by editors in Chief from Geographical Journals [J]. Acta Geographica Sinica, 2005, 60(4): 531‒545.

[84]   Hu, H. Y. Essays on China??s Population Distribution [M]. Shanghai: East China Normal University Press, 1983.

[85]   Ding, J. H., Liu, Z. Y., Cheng, D. M., et al. Areal differentiation of inter-provincial migration in China and characteristics of the flow field [J]. Acta Geographica Sinica, 2005, 60(1): 106‒114.

[86]   Ge, M. L., Feng, Z. M. Research on the distribution pattern of China??s population in 2000 Based on GIS: compared with Hu Huanyong??s research in 1935 [J]. Population Research, 2008, 32(1): 51‒57.

[87]   Liu, S. H., Deng, Y., Hu, Z. Research on classification methods and spatial patterns of the regional types of China??s floating population [J]. Acta Geographica Sinica, 2010, 65(10): 1187‒1197.

[88]   Qi, W., Liu, S. H., Zhao, M. F. Study on the stability of Hu Line and different spatial patterns of population growth on its both sides [J]. Acta Geographica Sinica, 2015, 70(4): 551‒566.

[89]   Lu, D. D., Wang, Z., Feng, Z. M., et al. Academic debates on Hu Huanyong population line [J]. Geographical Research, 2016, 35(5): 805‒824.

[90]   Chen, M. X., Li, Y., Gong, Y. H., et al. The population distribution and trend of urbanization pattern on two sides of Hu Huanyong population line: a tentative response to Premier Li Keqiang [J]. Acta Geographica Sinica, 2016, 71(2): 179‒193.

[91]   Zhou, L. S. The Theory and Practice of Agricultural Regionalization in China [M]. Hefei: University of Science and Technology of China Press, 1993.

[92]   Liu, Y. S, Zhang, Z. W., Wang, J. Y. Regional differentiation and comprehensive regionalization scheme of modern agriculture in China [J]. Acta Geographica Sinica, 2018, 73(2): 203‒218.

[93]   Song, C. Q. On paradigms of geographical research [J]. Progress in Geography, 2016, 35(1): 1‒3.

[94]   Song, C. Q., Cheng, C. X., Shi, P. J. Geography complexity: New connotations of geography in the new era [J]. Acta Geographica Sinica, 2018, 73(7): 1204–1213.