1-km Grid Precipitation Dataset in the Three-River
Headwaters Region (2009?C2013)
Jiang, Y. H.1,2 Li, B. L.1,2* Yuan, Y. C.1 Gao, X. Z.1 Zhang, T.1,2 Liu, Y.1,2
Li, Y.1,2 Luo, Z. Y.3 Li, H.3 Ma, Q.3 Wang, X. M.3 Ciren, D. J.4
1. State Key Laboratory of Resources and
Environmental Information Systems, Institute of Geographic Sciences and Natural
Resources Research, Chinese Academy of Sciences, Beijing 100101, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Meteorological Bureau of Mongolian Autonomous
County of Henan, Tibetan Autonomous Prefecture of Huangnan, Huangnan 811599,
China;
4. Lhasa Meteorological Bureau, Lhasa 850000,
China
Abstract: This
dataset includes the downscaled Tropical Rainfall Measuring Mission (TRMM) 3B43
precipitation based on rainfall observations from rain gauges and related
contrasting or auxiliary data. Downscaled TRMM data was based on a quadratic
parabolic profile (QPP) model. This method involves two steps. (1) QPP model
parameters estimation. In Three-River Headwaters region, the elevation of
maximum precipitation corresponds to the elevation of maximum NDVI. Thus, the
elevation of maximum precipitation could be determined based on the spatial
location of the peak NDVI. Subsequently, estimating the
precipitation at the elevation of maximum precipitation as well as the
quadratic coefficients in parabolic equation of precipitation. (2)
Spatial extrapolation of model parameters. The parameters at 0.25?? resolution
are spatially extrapolated in inverse distance weighted interpolation. The
bilinear interpolation method is then employed to resample the parameters from
0.25?? to 1-km resolution to obtain the ultimate parameters of the downscaled
model for each pixel. The results show that downscaled TRMM 3B43 data in QPP
model are more accurate than those obtained in conventional statistical
downscaling methods. The average root-mean-square errors (RMSEs) and mean
absolute percent errors (MAPEs) calculated with national observation data from
May to September and growing season in 2009?C2013 are 14, 18, 19, 13, 16 mm and
14%, 12%, 12%, 12%, and 17%, respectively. The dataset is archived in the WGS84
coordinate system as vector data with a .shp format and raster data in a Grid
or .tif format.
Keywords: precipitation; TRMM satellite; downscaling; Three-River Headwaters
region and its nearby regions
Dataset Available
Statement:
The dataset supporting this paper
was published at: Jiang, Y. H., Li, B. L., Yuan, Y. C., et al. 1-km grid
precipitation dataset in the Three-River Headwaters region (2009?C2013) [J/DB/OL].
Digital Journal of Global Change Data Repository,
2019. DOI: 10.3974/geodb.2019.05.17.V1.
1 Introduction
Precipitation,
an important environmental element, plays a role not to be overlooked in areas
such as surface runoff, atmospheric motions, and agricultural resources.
However, due to the randomness, precipitation exhibits relatively complex
temporal and spatial variation patterns. It is difficult to extrapolate
precipitation observation data acquired at the limited number of ground
stations, particularly in regions with relatively few stations. Satellite remote
sensing products cover large areas and consist of repeated observations. As a
consequence, satellite remote sensing has become an important means for
acquiring information on temporal and spatial variations of precipitation.
However, due to such factors as topography, precipitation in mountainous
regions exhibits notable heterogeneity. As a result, satellite precipitation
data for mountainous regions are of extremely high uncertainty and unable to
meet the actual requirements[1?C3].
In view of this, a finer precipitation dataset was developed in this study by
spatial downscaling of precipitation data retrieved from satellite remote
sensing data.
??1-km grid precipitation dataset in the Three-River
Headwaters region (2009?C2013)??[4]
was produced using
the widely available TRMM 3B43 V7 data product (0.25????0.25??)[5?C6].
The TRMM data product in Three-River Headwaters region is of relatively low accuracy,
and to solve the problem, assuming that precipitation is jointly determined by
macroscopic geographical factors and local elevations, and there is a strong
correlation between normalized difference vegetation index (NDVI) and precipitation
in the region. Under these assumptions, a quadratic parabolic profile (QPP)
model was employed to downscale the TRMM data. The parameters of the
relationship between NDVI and digital elevation model (DEM) were determined
based on high-resolution NDVI data, then to estimate the parameters between DEM
and precipitation. Finally, downscaled TRMM precipitation data was based on the
high-resolution DEM data[3]. The
revised product is compared with the results generated from the ground site
interpolation method for validation.
2 Metadata of the
Dataset
The metadata of
the ??1-km grid precipitation dataset in the Three-River Headwaters region
(2009?C2013)??[4] is summarized in
Table 1. It includes the dataset full name, short name, authors, year, temporal
resolution, spatial resolution, data format, data size, data files, data
publisher, data sharing policy, etc.
3 Method
3.1 Algorithm
According
to the theory of precipitation in mountainous established by Fu[8],
precipitation in a mountainous region is jointly determined by precipitation
affected by macroscopic geographic factors and precipitation variation
resulting from the difference in local elevation, and can thus be represented
and calculated by a parabolic equation. The elevation difference of region is
large, and precipitation in this area is greatly affected by the terrain, which
satisfies the application condition of parabolic equation. In the studying
region, the annual average precipitation is less than 1,000 mm, and
precipitation has a positive correlation wtih NDVI in such region when
excluding the effects of local topography. Therefore, the same function should
fit the relationships between elevation and precipitation or NDVI. When not
taking into consideration the effects of local topography, there is a positive
correlation between precipitation and vegetation growth in sub-humid and
semiarid regions, which can be represented by the linear response relationship
between precipitation and NDVI[9-10]. Hence, algorithm used in this study is to assume that
both precipitation and NDVI are in a quadratic parabolic relationship with
elevation. The parameters of the NDVI?CDEM function
Table 1 Metadata summary of the dataset
|
Items
|
Description
|
|
Dataset full name
|
1-km grid precipitation dataset in the Three-River Headwaters region (2009?C2013)
|
|
Dataset short name
|
PrecipThreeRiverHeadwaters_2009-2013
|
|
Authors
|
Jiang, Y. H. N-8765-2019, Institute of Geographic Sciences
and Natural Resources Research, ChineseAcademy of Sciences,
jiangyh@lreis.ac.cn
Yuan, Y. C. N-9047-2019, Institute of Geographic Sciences
and Natural Resources Research, Chinese Academy of Sciences,
yuanyc@lreis.ac.cn
Gao, X, Z. N-1655-2019, Institute of Geographic Sciences
and Natural Resources Research, Chinese Academy of Sciences,
gaoxz@lreis.ac.cn
Zhang, T. N-8690-2019, Institute of Geographic Sciences
and Natural Resources Research, Chinese Academy of Sciences, zhangtao@lreis.ac.cn
Liu, Y. N-8844-2019, Institute of Geographic Sciences and
Natural Resources Research, Chinese Academy of Sciences, liuy.18b@igsnrr.an.c.cn
Li, Y. Y-4384-2019, Institute of Geographic Sciences and
Natural Resources Research, Chinese Academy of Sciences, liying9391@126.com
Luo, Z. Y., Meteorological Bureau of Mongolian Autonomous
County of Henan, Tibetan Autonomous Prefecture of Huangnan, 393352158@qq.com
Li, H., Meteorological Bureau of Mongolian Autonomous
County of Henan, Tibetan Autonomous Prefecture of Huangnan, lh691208@163.com
Ma, Q., Meteorological Bureau of Mongolian Autonomous
County of Henan, Tibetan Autonomous Prefecture of Huangnan, 107082968@qq.com
Wang, X. M., Meteorological Bureau of Mongolian Autonomous
County of Henan, Tibetan Autonomous Prefecture of Huangnan, 2444869807@qq.com
Ciren, D. J., Lhasa Meteorological Bureau,
LSNSE111@126.com
|
|
Geographical region
|
31.65??N?C36.27??N, 89.40??E?C102.38??E,
including 16 counties and one town in central and southern Qinghai: Xinghai county,
Zekog county, Henan county, Gade county, Maqin county, Banma county, Yushu
Tibetan autonomous prefecture, Chindu county, Zadoi county, Zhidoi county,
Madoi county, Qumarleb county, Nangqen county, Dari county, Jiuzhi county,
Tongde county, Tanggula town
|
|
Year
|
2009?C2013 Temporal
resolution 1 month Spatial resolution 1 km
|
|
Data format
|
.shp, .tif, .grid
Data size 344 MB (compressed)
|
|
Dataset
files
|
The dataset consists of four folders.
(1) The ??QPR_Precip?? folder contains 5.Grid files:
QPR_2009, QPR_2010, QPR_2011, QPR_2012 and QPR_2013 are
downscaled TRMM 3B43 cumulative precipitation (unit: mm) in QPP model for
May, June, July, August, September, and the growing season of 2009, 2010,
2011, 2012 and 2013, respectively
(2) Control_Precip folder contains 15.Drid files:
?? ER_2009, ER_2010, ER_2011, ER_2012 and
ER_2013 are downscaled TRMM 3B43 cumulative precipitation (unit: mm) in for
exponential regression (ER) model May, June, July, August, September, and the
growing season of 2009, 2010, 2011, 2012 and 2013, respectively
?? MLR_2009, MLR _2010, MLR _2011, MLR
_2012 and MLR _2013 are downscaled TRMM 3B43 cumulative precipitation (unit:
mm) in multiple linear regression (MLR) model for May, June, July, August,
September, and the growing season of 2009, 2010, 2011, 2012 and 2013,
respectively
?? GWR_2009, GWR_2010, GWR_2011, GWR_2012
and GWR_2013 are downscaled TRMM 3B43 cumulative precipitation (unit: mm) in
geographically weighted regression (GWR) model for May, June, July, August,
September, and the growing season of 2009, 2010, 2011, 2012 and 2013,
respectively
(3) DEM file contains a .Grid file named dem1km, which is
the information on elevation variation within the study area
|
|
|
(4) NDVI folder contains five .grid files named
ndv1km_2009, ndv1km_2010, ndv1km_2011, ndv1km_2012, and ndv1km_2013, which
are vegetation growth data for the growing season of 2009, 2010, 2011, 2012,
and 2013, respectively
|
|
Foundations
|
Ministry of
Science and Technology of P. R. China (2016YFC0500205, 2015CB954103)
|
|
Computing Enviroment
|
Python 2.7; ArcGIS campus license of Institute of Geographical Sciences and Natural
Resources Research, Chinese Academy of Sciences
|
|
Data publisher
|
Global Change Research Data
Publishing & Repository, http://www.geodoi.ac.cn
|
|
|
|
(To be continued on the next
page)
(Continued)
|
Items
|
Description
|
|
Address
|
No.
11A, Datun Road, Chaoyang District, Beijing 100101, China
|
|
Data sharing policy
|
Data from the Global Change Research Data
Publishing & Repository includes metadata, datasets (in the Digital Journal of Global
Change Data Repository), and publications (in the Journal of Global
Change Data & Discovery). Data sharing policy includes: (1) Data
are openly available and can be free downloaded via the Internet; (2) End
users are encouraged to use Data subject to citation; (3)
Users, who are by definition also value-added service providers, are welcome
to redistribute Data subject to written permission from the GCdataPR Editorial
Office and the issuance of a Data redistribution license; and (4)
If Data
are used to compile new datasets, the ??ten per cent principal?? should be
followed such that Data records utilized should not
surpass 10% of the new dataset contents, while sources should be clearly
noted in suitable places in the new dataset[7]
|
|
Communication and searchable system
|
DOI, DCI, CSCD, WDS/ISC, GEOSS, China GEOSS, Crossref
|
|
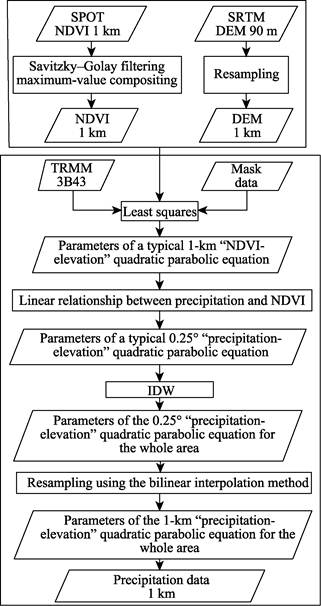
Figure 1 Technical route for
the dataset development
|
are
first determined based on high-resolution NDVI and DEM data, then to estimate the parameters
between DEM and precipitation. Finally, downscaled TRMM precipitation
data was based on the high-resolution DEM data[3].
3.2 Technical Route
The
dataset was produced in TRMM data downscaling method that accounts for macroscopic
geographic factors and local elevations[3].
This method involves the following two main steps (Figure 1): (1) Estimation of
the QPP model parameters. Based on the assumption in the algorithm principle
that there are similar parabolic relationships between precipitation and
elevation or NDVI, the maximum precipitation should be at the location where
the peak NDVI occurs[9?C10]. (2)
Spatial extrapolation of model parameters. The parameters at 0.25?? resolution
are spatially extrapolated in inverse distance weighted interpolation. The
bilinear interpolation method is then employed to resample the parameters from
0.25?? to 1-km resolution to obtain the ultimate parameters of the downscaled model for each pixel.
4 Data Results and Validation
4.1 Data
Products
The dataset is composed of 4 folders (QPR_Precip,
Control_Precip, DEM and NDVI) as shown in
Table
1.
4.2 Data Results
DEM and NDVI
were shown in Figure 2-3. Precipitation data of July and growing season
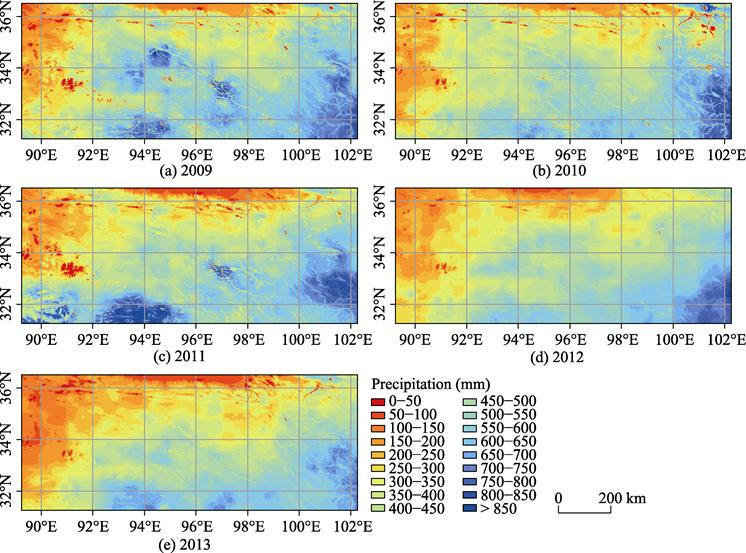
in the region between 2009 and 2013 were shown in Figure 4-5.
As shown in Figure 2, the elevation in Three-River
Headwaters region gradually increases from southeast to northwest. A decrease
trend of growing season NDVI can be observed in Figure 3 from southeast to
northwest.
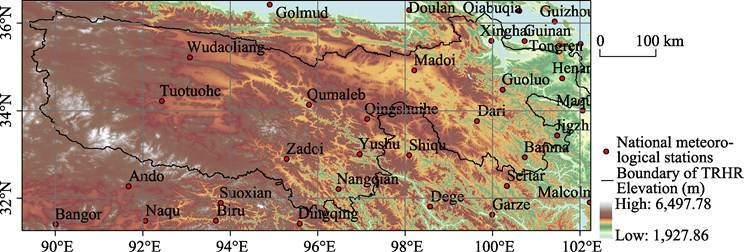
Figure 2 DEM and spatial
distribution of national meteorological stations in the Three-River Headwaters
region
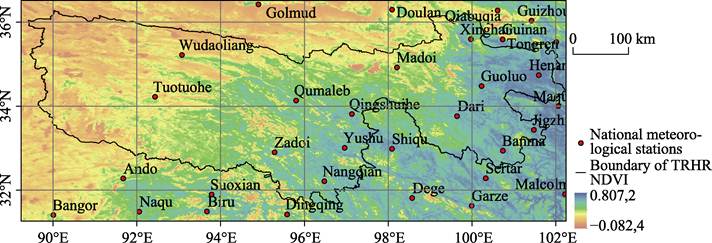
Figure 3 Spatial distribution
of NDVI in the Three-River Headwaters region in the growing season of 2012
In
Figures 4 and 5, precipitation of July and the whole growing season in this
region mainly gradually decreases from southeast to northwest, which
corresponds to the topography and the direction of water vapor (southeast
monsoon) in Three-River Headwaters region. Locally, the maximum precipitation
often occurs on mountain slopes instead of valleys, and this corresponds to the
theory of maximum precipitation elevations.
4.3 Validation of Data
Results
![??????: Table 2 Average RMSEs and MAPEs be-tween the downscaled data and observation data acquired at national stations for the growing season in the period 2009?C2013[3]
Month RMSE (mm) MAPE (%)
May 14 14
June 18 12
July 19 12
August 13 12
September 16 17
Cumulative 62 11](http://geodoi.ac.cn/DOIPaper/ENHTML/2020139402\202002139409.files/image007.png) Mean Absolute Error (MAE) and Mean
Absolute Percent Error (MAPE) are the accuracy
evaluation indicator to test the accuracy of the downscaled TRMM monthly and cumulative
precipitation data for the growing season in the period 2009?C2013. The downscaled data are of
relatively high accuracy and can relatively satisfactorily meet the accuracy requirements
of relevant research for the spatial and
temporal distribution patterns of precipitation (Table 2).
Mean Absolute Error (MAE) and Mean
Absolute Percent Error (MAPE) are the accuracy
evaluation indicator to test the accuracy of the downscaled TRMM monthly and cumulative
precipitation data for the growing season in the period 2009?C2013. The downscaled data are of
relatively high accuracy and can relatively satisfactorily meet the accuracy requirements
of relevant research for the spatial and
temporal distribution patterns of precipitation (Table 2).
5 Discussion and
Conclusion
The dataset generation algorithm in this
study primarily takes into account the mechanism of formation of precipitation
in mountainous regions[8]. Based
on the theory of maximum precipitation elevations and the linear response relationship
between NDVI and precipitation, the TRMM precipitation data for Three-River
Headwaters region were downscaled to
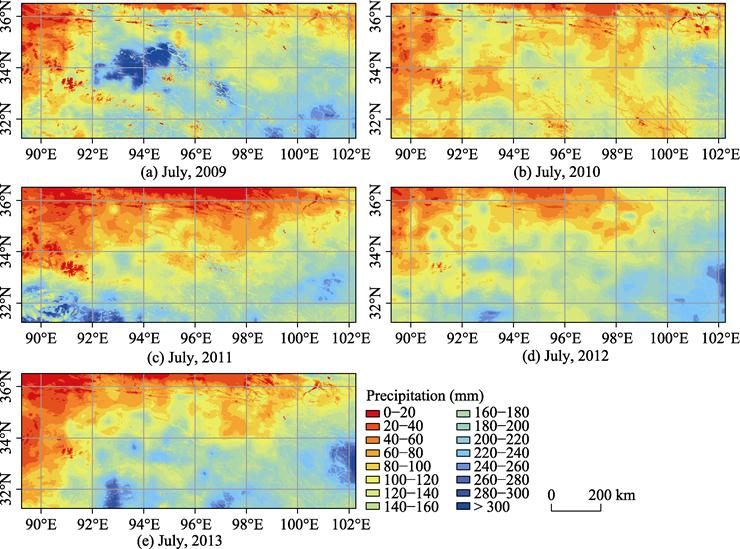
Figure 4 Spatial distribution of precipitation
in the Three-River Headwaters region in July in the period 2009?C2013
Figure
5 Spatial distribution of precipitation
in the Three-River Headwaters region in the growing season in the period
2009?C2013
improve their accuracy and
provide a more accurate data product for analyzing the temporal
and spatial distribution
patterns of precipitation. A notable decrease is found in the simulated regional
precipitation from southeast to northwest, which corresponds to the topography
and
the direction of water
vapor (southeast monsoon) in Three-River Headwaters region. Locally, the
maximum precipitation often occurs on mountain slopes instead of valleys, and
this corresponds to the theory of maximum precipitation elevations. The errors
of the downscaled data are also within a reasonable range, and these data can
meet the requirements of regional hydrological research.
The shortcomings of the algorithm
in this study were not take into consideration the topographical and geomorphic
factors of Three-River Headwaters region, and also neglected solid
precipitation. Potential impact includes: (1) Ignoring the different effects of
terrain uplift on precipitation on the windward and leeward slopes; (2) This
algorithm is only applicable in downscaling of growing-season precipitation,
and was not for solid precipitation in winter, thus was unable to generate precipitation
data for the whole year. Additionally, the accuracy of downscaled data is
significantly affected by the accuracy of the original product. If the
pre-downscaling precipitation data contain large errors, the accuracy of the
downscaled data product will remain inadequate. Therefore, this algorithm will
give rise to significant uncertainties when used in application research that
requires relatively high accuracy in absolute precipitation.
Author Contributions
Li, B. L. and Jiang, Y. H.
developed the overall technical route for the data collection; Liu, Y. and Li,
Y. processed the TRMM precipitation data; Zhang, T. and Yuan, Y. C. designed
the model and algorithm; Gao, X. Z. performed data verification; Luo, Z. Y.,
Li, H., Ma, Q., Wang, X. M. and Ciren, D. J. provided the weather station data.
Jiang, Y. H. and Li, B. L. wrote the data paper.
References
[1]
Hao, Z. C.,
Tong, K., Zhang, L. L., et al. Applicability analysis
of TRMM precipitation estimates in Tibetan Plateau [J]. Water, 2011,
31(5): 18?C23.
[2]
Liu, Y. B., Fu, Q. N., Song, P., et al. Satellite retrieval of precipitation: a review [J]. Advance in Earth Sciences, 2011, 26(11):
1162?C1172.
[3]
Zhang, T., Li, B. L., Yuan, Y. C., et al. Spatial downscaling of TRMM precipitation data considering
the impacts of macro-geographical factors and local elevation in the Three-River
Headwaters region [J]. Remote Sensing of
Environment, 2018, 215: 109?C127.
[4]
Jiang, Y. H., Li, B. L., Yuan, Y. C., et al. 1-km grid precipitation dataset in the Three-River Headwaters
region (2009?C2013) [J/DB/OL]. Digital
Journal of Global Change Data Repository, 2019. DOI: 10.3974/geodb.2019.05.17.V1.
[5]
Kummerow,
C., Barnes, W. The tropical rainfall measuring mission (TRMM) sensor package
[J]. Journal of Atmospheric and Oceanic
Technology, 1998, 15: 809?C817.
[6]
Huffman, G.
J., Bolvin, D. T., Nelkin, E. J., et al.
The TRMM multisatellite precipitation analysis (TMPA): quasi-global, multiyear,
combined-sensor precipitation estimates at fine scales [J]. Journal of Hydrometeorology, 2007, 8(1):
38?C55.
[7]
GCdataPR Editorial Office. GCdataPR data
sharing policy [OL]. DOI: 10.3974/dp.policy.2014.05 (Updated 2017).
[8]
Fu, B. P.
Mountain climate [M]. Beijing: Science Press, 1983.
[9]
Groeneveld,
D. P., Baugh, W. M. Correcting satellite data to detect vegetation signal for
eco-hydrologic analyses [J]. Journal of Hydrology, 2007, 344(1/2): 135?C145.
[10]
Chamaille-Jammes,
S., Fritz, H., Murindagomo, F. Spatial patterns of the NDVI?Crainfall
relationship at the seasonal and interannual time scales in an African savanna
[J]. International Journal of Remote Sensing, 2006, 27(23): 5185?C5200.